A New Mathematical Operating System for AI

From Flat Gradients to Jet Geometry: Differentiating the Space Instead of the Network

AI without an OS. GIF created by the author with Blender.

TL;DR

Most current AI runs on a flat, first-order OS: everything is a tensor in R^n, and training is driven primarily by first-order gradients. If you want anything richer—HVPs, curvature signals, better memory, you have to stack grad, jacfwd, jacrev, jvp, vjp and manage extra graphs, extra passes, and extra bugs. The result in practice: unstable training, brittle generalization, and ugly workarounds for hierarchy (hyperbolic “patches”) and memory (KV caches, ad-hoc recurrence).

This post proposes a new mathematical OS for AI: instead of differentiating the program, we differentiate the space. Internal states are jets on curved manifolds (hyperbolic for hierarchy, toroidal for phase/memory). A single pass on jet-valued states gives you value, gradient, and useful second-order information along the encoded directions as one object, and standard AD primitives (JVP, VJP, HVP) can be understood as consequences of the jet algebra and its functoriality. For AI engineers, this means:

• geometry and hierarchy built into the representation space,

• structured, low-interference memory from topology,

• higher-order training signals available by changing the state type, not by wiring up new AD pipelines.

1. Introduction

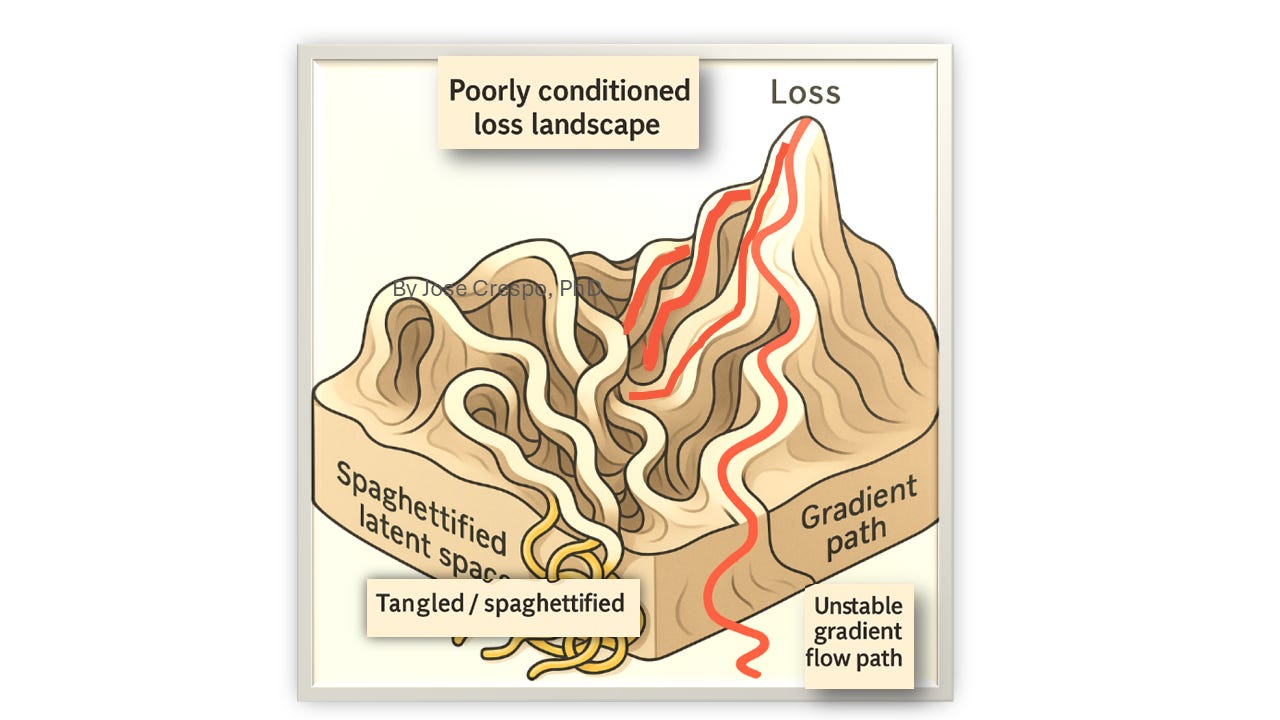
Modern AI runs in what we will call the Euclidean first-order regime. Internal states are flat tensors in R^n, and training is driven almost entirely by first-order gradients in those coordinates. Contemporary automatic differentiation (AD) frameworks compute these gradients exactly on their primitives (up to floating-point error), but they do so as transformations on tensor programs— grad, jacfwd, jacrev, jvp, vjp —each of which can be viewed as defining a new graph in flat space. Large-scale optimization then unfolds on poorly conditioned Euclidean landscapes, and as models grow, we repeatedly see unstable gradients, tangled latent trajectories, memory interference, and brittle compositional behavior.

We treat these not as incidental engineering glitches, but as signs that the underlying mathematical substrate is misaligned with the phenomena we want to model.

This article proposes a different substrate: a geometric, jet-based operating system for AI. Instead of keeping states as points in R^n and repeatedly differentiating the program, we differentiate the space itself.


Internal states are jets on curved manifolds: truncated Taylor expansions living in Jk(M), with M (i.e. Toroid or Hyperbolic) chosen to match the semantics of the task—for example, hyperbolic manifolds for hierarchical representations and tori for periodic, phase-like memory. Dual numbers and higher-order jet algebras provide an intrinsic semantics for differentiation: a single semantic pass through the network propagates jet-valued states via the functorial jet-lift Jk(F), so value, gradient, and selected low-order higher-derivative information along the encoded directions appear as components of one geometric object rather than as separate AD constructions.

From this viewpoint, hallucinations, gradient pathologies, “spaghettized” latents, and memory collisions are reinterpreted as consequences of forcing hierarchical, periodic, and higher-order structure into flat Euclidean embeddings while using almost exclusively first-order dynamics. By formulating differentiation and parameter updates at the level of jet functors, and by analyzing how curvature and topology shape the resulting flows, we argue that many weaknesses of current architectures arise from this flat, first-order foundation itself—and that a geometric, jet-based operating system for AI is a more appropriate starting point than further tuning of the existing one.

2. The Euclidean First-Order Regime

We begin by making precise what we mean by the Euclidean first-order regime that characterizes essentially all contemporary large-scale AI systems.

2.1. Representations as Euclidean tensors

Let X denote an input space (e.g. token sequences, images, or states), and let a model be a parametrized map:

\(\begin{array}{l} f_\theta : X \to Y, \\ \\ \text{implemented as a composition of } L \text{ layers} \\ \\ f_\theta = f_L \circ f_{L-1} \circ \cdots \circ f_1, \\ \\ \text{where each layer } f_\ell \text{ acts on a Euclidean space:} \\ \\ f_\ell : \mathbb{R}^{n_{\ell-1}} \to \mathbb{R}^{n_\ell}. \end{array}\)

\(\begin{array}{l} \text{In practice, these } \mathbb{R}^{n_\ell} \text{ are realized as high-dimensional tensors} \\ \text{(activations, attention states, key-value caches, etc.), but mathematically} \\ \text{they are flat vector spaces endowed with the standard Euclidean inner product.} \\ \\ \text{All internal representations can thus be written as a sequence} \\ \\ x_0 = \text{enc}(x), \quad x_\ell = f_\ell(x_{\ell-1}), \quad \ell = 1, \ldots, L, \\ \\ \text{with } x_\ell \in \mathbb{R}^{n_\ell}. \text{ There is no intrinsic curvature or topology beyond} \\ \text{that of } \mathbb{R}^{n_\ell}; \text{ any hierarchical, periodic, or discrete structure must be} \\ \textit{simulated} \text{ within this flat space by the choice of parametrization and} \\ \text{learned weights, rather than being enforced by the underlying geometry.} \end{array}\)

In the next subsection we will see that the same Euclidean assumption is inherited by the learning dynamics: automatic differentiation computes exact gradients of these tensor maps in flat coordinates, and optimization operates on this Euclidean parameter and representation space using almost exclusively first-order information.

2.2. First-order gradient dynamics

Training consists in minimizing an empirical loss

\(\mathcal{L}(\theta) = \frac{1}{N} \sum_{i=1}^{N} \ell(f_\theta(x_i), y_i)\)

\(\begin{array}{l} \text{over parameters } \theta \in \mathbb{R}^P, \text{ typically via (stochastic) gradient-based} \\ \text{methods. In continuous time, idealized gradient flow obeys} \\ \\ \frac{d\theta_t}{dt} = -\nabla_\theta \mathcal{L}(\theta_t), \end{array}\)

and practical algorithms such as SGD, Adam, or their variants implement discrete approximations of this ODE.

\(\begin{array}{l} \text{Modern frameworks compute } \nabla_\theta \mathcal{L}(\theta) \text{ by reverse-mode automatic} \\ \text{differentiation. If we denote by } J_\ell(x_{\ell-1}) = Df_\ell(x_{\ell-1}) \text{ the Jacobian of layer } f_\ell, \\ \text{then by the chain rule} \\ \\ Df_\theta(x_0) = J_L(x_{L-1}) J_{L-1}(x_{L-2}) \cdots J_1(x_0), \\ \\ \text{and the gradient with respect to parameters of an early layer has the} \\ \text{schematic form} \\ \\ \frac{\partial \mathcal{L}}{\partial \theta^{(i)}} = \frac{\partial \mathcal{L}}{\partial x_L} \left(\prod_{\ell=i}^{2} \frac{\partial x_\ell}{\partial x_{\ell-1}}\right) \frac{\partial x_1}{\partial \theta^{(i)}}. \end{array}\)

In exact arithmetic, this gradient is mathematically exact: no finite-difference limits are taken, and the derivatives of the primitives are analytic. However, the dynamics of θt\theta_tθt​ under these gradients are governed by the geometry of a high-dimensional loss surface embedded in a flat parameter space RP\mathbb{R}^PRP.

Two structural features follow:

\(\begin{array}{l} \textbf{First-order locality.} \text{ The default update at time } t \text{ depends only on } \theta_t \\ \text{and the first derivative } \nabla_\theta \mathcal{L}(\theta_t). \text{ While higher-order information} \\ \text{(e.g. Hessian--vector products) can be computed exactly via additional AD} \\ \text{transforms, it appears as an optional, derived operation rather than as part of} \\ \text{the native state representation, and is rarely used systematically at scale.} \\ \\ \textbf{Euclidean embedding.} \text{ Both parameters and activations live in Euclidean} \\ \text{spaces with the standard linear structure. Any nontrivial geometry---hierarchical,} \\ \text{periodic, or topological---must emerge from the learned weights rather than} \\ \text{being enforced by the ambient space.} \end{array}\)

2.3. Geometric and numerical failure modes

Within this Euclidean first-order regime, well-known pathologies can be interpreted as geometric and numerical phenomena:

\(\begin{array}{l} \textbf{Vanishing and exploding gradients.} \\ \text{The product of Jacobians} \\ \\ J_L J_{L-1} \cdots J_1 \\ \\ \text{tends to contract or expand along typical directions depending on the spectral} \\ \text{properties of the } J_\ell. \text{ In deep networks, this leads to gradients whose norms} \\ \text{decay toward zero or blow up exponentially with depth. This behavior is intrinsic} \\ \text{to the composition of linear maps in a flat space; it is not a defect of automatic} \\ \text{differentiation itself.} \\ \\ \end{array}\)

\(\begin{array}{l} \textbf{Ill-conditioning and tangled trajectories.} \\ \text{The Hessian } \nabla_\theta^2 \mathcal{L}(\theta) \text{ in } \mathbb{R}^P \text{ is often highly anisotropic, with} \\ \text{eigenvalues spanning many orders of magnitude. Gradient flow then follows} \\ \text{narrow, curved valleys in parameter space, and small perturbations in } \theta \text{ or} \\ \text{in activations } x_\ell \text{ can lead to macroscopically different behaviors. This} \\ \text{manifests as } \textbf{spaghettized latent spaces}, \text{ where semantically related states} \\ \text{are neither linearly nor geodesically well-organized.} \end{array}\)

• Memory interference.
  In recurrent architectures and transformer key–value caches, different histories are encoded as trajectories in a shared Euclidean latent space. Without any topological notion of “distinct memories,” trajectories corresponding to different sequences can intersect, overlap, or collapse onto nearby regions, leading to interference and collisions in retrieval and generation.

• Brittle compositional behavior and hallucination.
  Since all structure is represented in a flat vector space and learning is driven by local first-order updates, there is no guarantee that compositional relations (e.g. hierarchy, nested scope, periodic structure) are preserved under extrapolation. The model may fit training statistics while mapping novel compositions to geometrically arbitrary regions of latent space, resulting in incoherent or fabricated outputs.

Figure 1. Anisotropic loss landscape for Euclidean first-order learning.

We do not claim that these phenomena can be uniquely or exhaustively explained by geometry alone, nor that curvature and topology are sufficient remedies. However, we take the above as evidence that the combination of (i) Euclidean representation spaces and (ii) purely first-order optimization constitutes a rigid and fragile foundation for intelligence at scale. The remainder of this work develops an alternative substrate—jets on curved manifolds—in which higher-order structure, curvature, and topology are built into the objects being optimized, rather than retrofitted as after-the-fact regularizers or architectural hacks.

2.4 The Hidden Geometry of Neural Networks (the smoking gun )


Up to now we have treated the Euclidean first-order regime as a design choice:

1. Representations as Euclidean tensors (Section 2.1):
   All internal states live in a single global coordinate chart R^n. No intrinsic structure—hierarchy, orientation, periodicity—is carried by the space itself.

2. Training as first-order gradient flow (Section 2.2):
   Optimization dynamics unfold in a flat parameter space R^P, driven almost exclusively by first-order derivatives computed in Euclidean coordinates.

3. Failure modes arising from this flatness (Section 2.3):
   Memory interference, unstable trajectories, brittle composition, and hallucinations emerge when complex structure is forced into a space with no geometry to support it.

What is less widely appreciated—and central to the foundational critique of this OS—is that even in this flat R^n setting, modern neural networks do not remain geometrically flat.
The geometry cannot be avoided.

Even when everything is implemented in flat R^n, modern neural networks already induce a nontrivial connection, and in practice exhibit nonzero curvature observable directly in their Jacobians.
The Euclidean OS is geometrically broken by its own internal transformations.

Here are the mathematical “tools” for visualizing those hidden curvatures in current AI frameworks:

2.4.1. The Jacobian as a Transport Map

\(\begin{array}{l} \text{Consider a single network block } F : X \mapsto Y. \\ \text{Given hidden states } (X_i) \text{ and outputs } (Y_j), \text{ automatic differentiation computes} \\ \text{the Jacobian blocks} \\ \end{array}{l}\)

Now we take a single frozen block

\(\begin{array}{l} F : X \mapsto Y, \\ \\ \text{acting on its internal representations. Let } X = (X_i)_{i \in B} \text{ and } Y = (Y_j)_{j \in B}, \\ \text{where } B \text{ indexes sites (tokens, patches, slots, or world-cells).} \\ \\ \text{Automatic differentiation computes the Jacobian blocks} \\ \\ \Gamma_{ij} = \frac{\partial Y_j}{\partial X_i}, \\ \\ \text{in standard Euclidean coordinates.} \end{array}\)

From an optimization standpoint, these blocks are used to assemble gradients. From a geometric standpoint, they encode something much stronger:

\(\begin{array}{l} \text{Each block } \Gamma_{ij} \text{ describes how an infinitesimal perturbation of the} \\ \text{representation at site } i \text{ influences the representation at site } j. \\ \text{Although computed purely for optimization, these blocks are in fact} \\ \textbf{parallel-transport operators between fibers:} \\ \\ \text{• each site } i \text{ carries a local representation space (fiber)} \\ \\ V_i \cong \mathbb{R}^d, \\ \\ \text{• and the Jacobian block} \\ \\ \Gamma_{ij} : V_i \to V_j \end{array}\)

In conclusion:

\(\begin{array}{l} \text{• each site } i \text{ carries a local representation space } V_i \cong \mathbb{R}^d, \\ \text{• and each block } \Gamma_{ij} : V_i \to V_j \text{ acts as a linear } \textbf{transport operator}, \\ \quad \text{describing how an infinitesimal perturbation at site } i \text{ is seen at site } j \\ \quad \text{after one block.} \\ \\ \text{The collection } \{\Gamma_{ij}\} \text{ can therefore be interpreted as a } \textbf{discrete } \mathbf{GL}(d)\text{-connection} \\ \text{on the fiber bundle} \\ \\ V = \coprod_{i \in B} V_i \longrightarrow B. \end{array}\)

So as you see we have the collection V to be connected via the transport operator Gamma

\(V = \coprod_{i \in B} V_i \longrightarrow B\)

where B again is the index set of sites (tokens, patches, slots, etc.).

This observation has been made explicit by Gardner (2024), but it also follows directly from the semantics of AD:
the representation graph becomes a connection graph, and the Jacobian blocks become its connection coefficients


2.4.2. Loops, holonomy, and curvature inside flat coordinates

Once transport maps exist, loops become meaningful.

\(\begin{array}{l} \text{Pick three sites } i, j, k \in B. \text{ Consider the oriented triangle} \\ \\ i \to j \to k \to i. \\ \\ \text{The induced parallel transport around this loop is the product} \\ \\ H_{ijk} = \Gamma_{ki} \circ \Gamma_{jk} \circ \Gamma_{ij}. \\ \\ \text{This linear operator } H_{ijk} : V_i \to V_i \text{ is the } \textbf{holonomy} \text{ of the induced connection} \\ \text{on that loop:} \\ \\ \text{• if } H_{ijk} = I, \text{ vectors transported around the loop return unchanged} \\ \quad \rightarrow \text{ locally flat on that triangle;} \\ \text{• if } H_{ijk} \neq I, \text{ vectors return rotated or sheared } \rightarrow \textbf{ nonzero discrete curvature} \\ \quad \text{and } \textbf{path-dependent transport}. \end{array}\)

Crucially, all of this happens inside the supposedly flat coordinates of R^n. There is no curved manifold in the architecture, no Riemannian layer, no special geometry—just the Jacobian of the block you already run.

The network pretends to occupy flat R^n,
but its own Jacobian-level transport shows that it behaves, operationally, like a non-flat connection on a bundle.

Figure 2. Curvature Hiding in Plain Sight: Holonomy Inside a Flat Euclidean Network.

Here is where the model’s curvature is created: Jacobian transport around loops of tokens reveals non-trivial curvature in the network’s internal geometric structure:

Figure 3. Holonomy in Action.

For a much deeper mathematical explanation, I strongly recommend you read my other two articles about:

Holonomy I

Holonomy II

3.From emergent curvature to designed geometry: Jets and Curved Manifolds as a Computational Substrate

This is the point at which the foundations crack.

If every serious neural model already defines a connection and empirically exhibits curvature through its Jacobians, then the real architectural choice is not:

• Euclidean vs geometric methods,

but:

• accidental geometry vs designed geometry.

\(\begin{array}{l} \text{The remainder of this work pursues the second option: we move from tensors in } \mathbb{R}^n \\ \text{to } \textbf{jets on curved manifolds } \mathcal{J}^k(M), \text{ and from emergent, opaque curvature to} \\ \textbf{explicit geometric structure} \text{ built directly into the state space.} \end{array}\)

\(\begin{array}{l} \text{which act as linear transport maps } \Gamma_{ij} : V_i \to V_j \text{ between local representation} \\ \text{fibers } V_i \cong \mathbb{R}^d. \text{ Taken together, these maps form a discrete } \mathbf{GL}(d)\text{-connection} \\ \text{on the bundle } \coprod_{i \in B} V_i \to B. \end{array}\)

Having identified the structural limitations of the Euclidean first-order regime, we now introduce the central objects of our alternative architecture: jets on curved manifolds. These objects unify representation, memory, and differentiation within a single geometric–algebraic framework.

Figure 4. Geometric Foundations—Why Jets on Curved Manifolds

3.1. From points to jets

\(\begin{array}{l} \text{In standard deep learning, the internal state of a model at layer } \ell \text{ is a point} \\ \\ x_\ell \in \mathbb{R}^{n_\ell} \end{array}\)

This representation encodes no intrinsic derivative or neighborhood structure; all higher-order information must be inferred implicitly through training, typically with only first-order gradients.

We instead represent an internal state not by a point but by a jet:

\(\begin{array}{l} \mathcal{J}_x^k(M) = \text{ the order-}k \text{ truncated Taylor expansion of a curve through } x \in M \end{array}\)

where M is a smooth manifold (hyperbolic or toroidal in our setting). A jet encodes:

• zeroth-order information (the point x),

• first-order information (the tangent vector),

• higher-order derivatives (curvature, torsion, etc., up to order k).

Jets can be realized algebraically using:

• dual numbers for k=1

• higher-order dual numbers / truncated polynomial rings for general kkk.

Thus, each internal state carries an intrinsic local Taylor model of itself.
This replaces the “pointwise” representation of modern networks with a much richer local geometric object.

3.2. Hyperbolic manifolds for representation

\(\begin{array}{l} \text{Representations of linguistic, visual, and conceptual structure often exhibit} \\ \textbf{hierarchical} \text{ or } \textbf{tree-like} \text{ structure. Hyperbolic manifolds } \mathbb{H}^n, \text{ with constant} \\ \text{negative curvature, are particularly well-suited for such structure due to:} \end{array}\)

• exponential volume growth with radius,

• natural embeddings of trees into geodesics,

• concentration of distances that reflect semantic hierarchy.

\(\begin{array}{l} \text{In our architecture, the representation layers } R_\ell \text{ are modeled as submanifolds} \\ \text{of a hyperbolic space, and the jets } \mathcal{J}_x^k(\mathbb{H}^n) \text{ describe not only a position in} \\ \text{hierarchy but local geometric structure (e.g., curvature of the representation} \\ \text{trajectory).} \end{array}\)

The manifold geometry thus organizes feature structure, rather than requiring the network to learn hierarchy from scratch inside a flat Euclidean space.

3.3. Toroidal manifolds for memory

Recurrent and stateful components of neural architectures (e.g., attention caches, recurrent channels) must maintain distinct trajectories for different sequences. In Euclidean latent spaces, trajectories can cross, collapse, or interfere, causing memory collisions or blending of contexts.

\(\begin{array}{l} \text{We instead model memory states on toroidal manifolds } \mathbb{T}^m = (S^1)^m, \\ \text{which naturally support:} \end{array}\)

• periodic structure,

• phase variables,

• winding numbers w∈Zmw \in \mathbb{Z}^mw∈Zm that serve as global, discrete invariants of recurrent dynamics.

A memory trajectory on a torus acquires a winding number vector that cannot be erased by smooth deformations. The pair

\((x, w) \in \mathbb{T}^m \times \mathbb{Z}^m\)

thus separates distinct histories even when their instantaneous positions are nearby.

\(\begin{array}{l} \text{When we augment toroidal memory with jets } \mathcal{J}_k^*(\mathbb{T}^m), \text{ additional local} \\ \text{Taylor-like data (jet coefficients) capture the } \textit{shape} \text{ of the trajectory around each} \\ \text{point, on top of its phase and winding class.} \end{array}\)

3.4. Differentiation as an intrinsic algebraic operation

In standard deep learning, differentiation is executed by an external automatic differentiation engine operating on Euclidean tensors. In contrast, jets carry their own algebraic differentiation structure:

• The first-order jet implements the chain rule via evaluation on dual numbers.

• Higher-order jets implement higher-order chain rules via truncated polynomial algebras.

• The tangent and cotangent lifts induced by jets correspond to Jacobian–vector products (JVPs) and vector–Jacobian products (VJPs), respectively.

• Hessian–vector products (HVPs) arise from functorial compositions JVP∘VJP and VJP∘JVP, depending on mode.
  

Thus, differentiation is reinterpreted not as a separate numerical pass over a computational graph, but as a native operation in the jet algebra of the manifold.

3.5. A categorical formulation

Jets and their transformations naturally form a category:

\(\begin{array}{l} \textbf{Objects:} \text{ jet bundles } \mathcal{J}^k(M) \text{ over manifolds } M. \\ \textbf{Morphisms:} \text{ smooth maps lifted to jets via their Taylor expansions.} \\ \textbf{Functors:} \\ \quad \text{• forward-mode AD corresponds to a jet-lifting functor } \mathcal{J}^k(f), \\ \quad \text{• reverse-mode AD corresponds to a cotangent-lifting functor,} \\ \quad \text{• their composition yields higher-order AD structures.} \end{array}\)

This categorical viewpoint unifies representation, memory, and differentiation under a single mathematical framework. Every component of the architecture—layers, updates, recurrences, memory—becomes explicitly geometric and functorial.

Summary of Section 3

Jets on curved manifolds replace the Euclidean first-order substrate with a geometric object that:

• encodes higher-order local information via truncated Taylor expansions,

• organizes representation via hyperbolic structure,

• organizes memory via toroidal topology and winding invariants,

• internalizes differentiation via jet algebra,and

• supports functorial composition for higher-order derivatives.

This sets the stage for Section 2, where we formalize JVP, VJP, and HVP as categorical transformations and show how learning dynamics on jet-valued states differ from their Euclidean first-order counterparts.

4.Bringing all components together within the framework of a new AI Operating System

The previous sections treated the pieces of the proposal in isolation: jets on curved manifolds as state, hyperbolic spaces for representation, tori for memory, and categorical differentiation as the core calculus. In this final section we reassemble them explicitly as an operating system for AI, and show how familiar OS notions map cleanly onto geometric objects and functors.

4.1. From operating systems to differential geometry

Figure 5 (“From Operating Systems to Differential Geometry”) is a small Rosetta stone. The left column lists standard OS concepts; the middle column shows the corresponding object in our framework; the right column explains why each mapping has a precise mathematical meaning.

Figure 5. they key parts of the AI OS

\(\begin{array}{l} \text{• } \textbf{Kernel type system } \to \textbf{ Category of geometric objects } \mathcal{C}. \\ \quad \text{The "types" of the kernel are not tensors but objects of a category: manifolds,} \\ \quad \text{bundles, hyperbolic/toroidal spaces, and their jet bundles. Morphisms are} \\ \quad \text{smooth maps (and their jet lifts). This is the universe in which all computations live.} \\ \\ \text{• } \textbf{Kernel primitive type } \to \textbf{ Jet-extended scalar / vector}. \\ \quad \text{Instead of plain } \mathbb{R} \text{ and } \mathbb{R}^d, \text{ the primitive values are elements of truncated} \\ \quad \text{polynomial rings like } \mathbb{R}[\varepsilon]/(\varepsilon^{k+1}) \text{ and their vector/bundle generalizations.} \\ \quad \text{Concretely: every scalar/vector carries its local jet (value plus derivatives up to} \\ \quad \end{array} \)

\( \begin{array}{l} \text{• } \textbf{System calls } \to \textbf{ Functorial operations}. \\ \quad \text{Operations such as } \texttt{LiftToJet}, \texttt{Diff}, \text{ or } \texttt{ParallelTransport} \text{ are endofunctors} \\ \quad \text{or natural transformations on } \mathcal{C}. \text{ A "syscall" is a request to apply a geometric} \\ \quad \text{functor: lift a map to jets, differentiate it, transport along a connection, and so on.} \\ \quad \text{This is where AD primitives (JVP, VJP, HVP) reappear in a structured way.} \end{array}\)

\(\begin{array}{l} \text{• } \textbf{Scheduler / execution model } \to \textbf{ Composition and jet propagation}. \\ \quad \text{The execution model is composition in the category } (g \circ f) \text{ together with the} \\ \quad \text{propagation of jets via} \\ \\ \quad \mathcal{J}^k(g \circ f) = \mathcal{J}^k(g) \circ \mathcal{J}^k(f). \\ \\ \quad \text{Associativity is guaranteed by the underlying algebra, not by ad-hoc graph rewriting.} \\ \\ \text{• } \textbf{Virtual memory \& addressing } \to \textbf{ Hyperbolic representation space } \mathcal{H}. \\ \quad \text{The "address space" for concepts is a Gromov-hyperbolic / Poincaré-type model} \\ \quad \text{where hierarchy is encoded geometrically. Distances, geodesics, and volume growth} \\ \quad \text{express tree-like structure that current models try to learn in a flat latent.} \\ \end{array}\)

\(\begin{array}{l} \text{• } \textbf{File system / persistence } \to \textbf{ Toroidal memory } \mathcal{M}. \\ \quad \text{Long-term memory lives on a torus } S^1 \times S^1 \times \ldots, \text{ where winding numbers} \\ \quad \text{and phases act as discrete indices and recurrence scaffolding. This yields a geometric} \\ \quad \text{notion of "address" and a memory layout designed to reduce interference.} \\ \\ \text{• } \textbf{Hardware abstraction layer } \to \textbf{ Backend functors}. \\ \quad \text{Backends like PyTorch or JAX are } \textit{modeled as} \text{ functors} \\ \\ \quad \text{Backend} : \mathcal{C} \longrightarrow \text{TensorsOn}(\text{PyTorch}/\text{JAX}/\ldots) \\ \\ \quad \text{that realize abstract geometric computations as concrete tensor programs, preserving} \\ \quad \text{composition and differentiation laws as closely as numerical implementations allow.} \end{array}\)

The point of the table is not metaphor. Each row replaces an OS-level abstraction by a well-defined geometric or categorical structure.

4.2. Geometric AI Operating System architecture

Figure 6 (“Geometric AI Operating System Architecture”) shows how these pieces stack into a full system.

Figure 6. Geometric AI Operating System Architecture.AI processes talk to a geometric kernel that treats toroidal memory, hyperbolic representation, and jet-based differentiation as OS-level primitives, while PyTorch, JAX, and similar frameworks sit below as interchangeable backend implementations. To really live inside this stack, today’s tensor libraries must be mathematically upgraded—their autodiff engines extended to support k-jet bundles, functorial Jacobian/Hessian operators, and holonomy-aware updates, instead of the current program-bound gradient hacks.

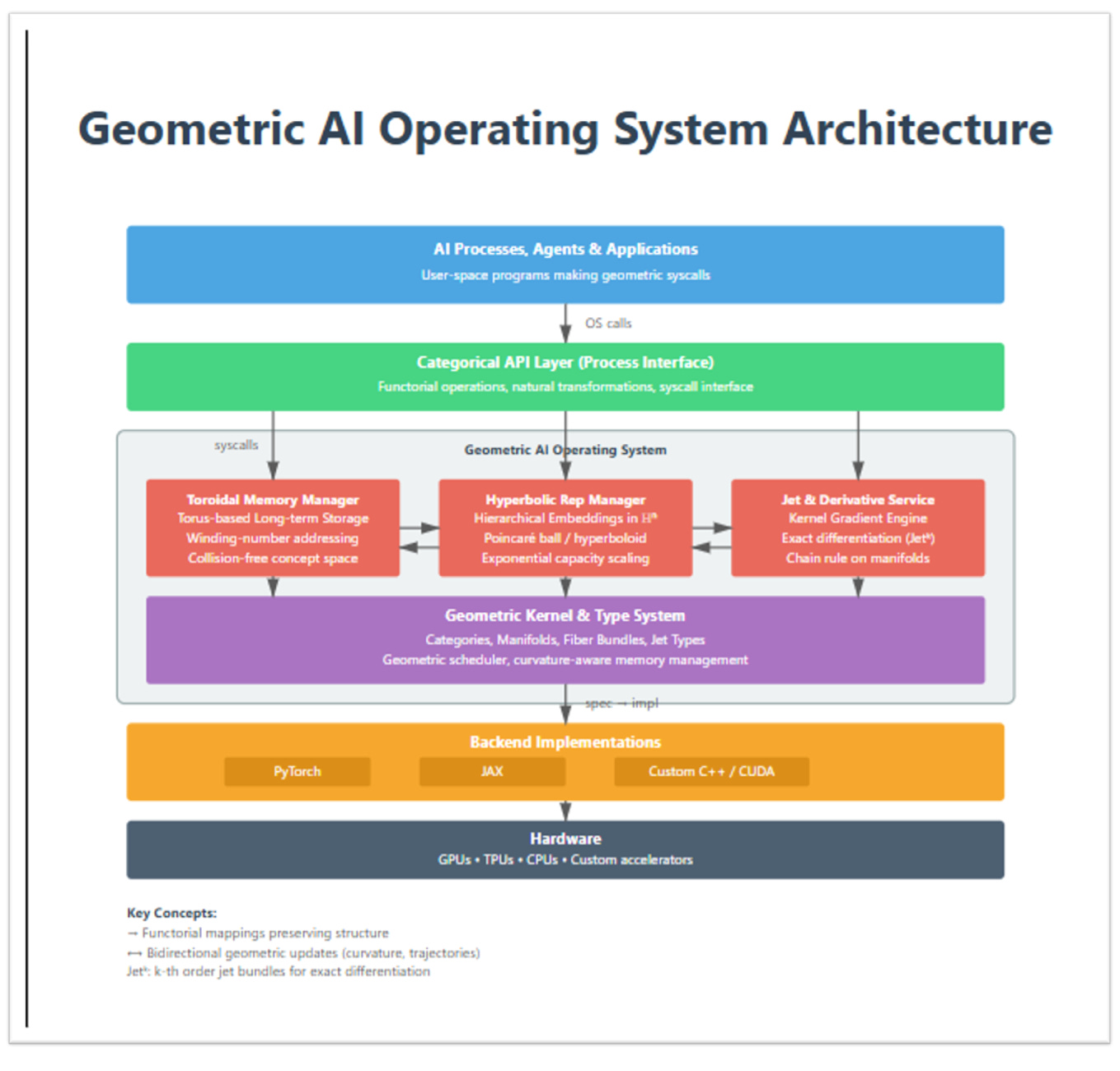
• User space: AI processes, agents, applications.
  At the top sit “programs” in the usual sense: agents, training loops, planning routines. They no longer speak tensors directly; they make geometric syscalls against an abstract API.

• Categorical API layer (process interface).
  This layer exposes functorial operations and natural transformations (LiftToJet, PushForward, PullBack, ParallelTransport, etc.). From a programmer’s point of view, this is the interface for “differentiate this map”, “transport along that trajectory”, or “read/write from toroidal memory”.

• Geometric AI Operating System (core services).
  Inside the OS box sit three main managers:

  • Toroidal Memory Manager - implements long-term storage on M, with winding-number addressing and interference-aware memory layouts.

  • Hyperbolic Representation Manager - manages embeddings in H, ensuring that hierarchical structure is aligned with the ambient negative curvature.

  • Jet & Derivative Service - the “gradient kernel”: it maintains jet-valued states, executes jet lifts J^k(F), and returns algebraically exact first-order and selected higher-order information (up to order k and floating-point error) in a single semantic pass.

  All three share a common view of state: everything is a jet on a chosen manifold, not a bare tensor.

• Geometric kernel & type system.
  Beneath the managers is the kernel itself: the category C of manifolds, bundles, and jet types, equipped with its scheduler (composition plus jet propagation) and curvature-aware memory logic. This is where the mathematics from Sections 2 and 3 lives.

• Backend implementations.
  PyTorch, JAX, and similar frameworks sit below as (ideally) interchangeable backend implementations. To really live inside this stack, today’s tensor libraries must be mathematically upgraded: their autodiff engines extended to support k-jet bundles, functorial Jacobian/Hessian operators, and holonomy-aware updates, instead of the current program-bound gradient pipelines built around stacked grad/jacfwd/jacrev transforms.

• Hardware.
  Finally, GPUs/TPUs/CPUs are just the physical substrate. The OS shields geometric code from hardware details in the usual way: we can, in principle, change accelerators without rewriting the mathematical layer.

4.3. What this buys you in practice

For AI practitioners, this “new OS” view is not an aesthetic indulgence; it changes what becomes easy:

• Higher-order information by construction.
  Because state is jet-valued, one semantic pass yields value, gradient, and chosen higher-order terms along encoded directions. Instead of stacking nested grad / jacfwd / jacrev transforms and maintaining multiple shadow graphs (as oddly happens now with PyTorch, JAX, etc.), a k-jet carries all the required order-k information in that single pass.

• Geometry-aligned representations.
  Hyperbolic and toroidal manifolds are not post-hoc interpretations but native spaces in which states live. Hierarchy, periodicity, and phase are expressed in the geometry, rather than being laboriously rediscovered in a flat latent.

• Structured memory and recurrence.
  Toroidal memory with winding-number addressing provides a geometric notion of index and cycle, giving a principled scaffold for long-range, repetitive, or phase-sensitive patterns.

• Backend independence as a design goal.
  Modeling backends as functors from the geometric category to tensors makes it possible, in principle, to swap PyTorch for JAX (or a future system) without changing the abstract OS logic. The mathematics and the implementation are cleanly separated.

• A principled handle on curvature and path-dependence.
  Curvature is no longer an accidental artifact glimpsed through occasional Jacobian probes; it becomes a first-class part of the state and connection. Tools like Gardner-style curvature heatmaps turn into diagnostics of the OS itself, not just of an opaque black box.

In short, the geometric AI operating system takes the hidden structure we already see leaking out of current models—curvature, gauge behavior, path-dependent transport—and promotes it to the level of design. Instead of asking flat tensors plus a first-order engine to simulate curved, higher-order phenomena, we build those phenomena into the substrate and let ordinary programming sit on top.