Hyperreal Programming in Action

How dual numbers, jets, and hyperreals fix broken AI

Nov 28, 2025

The Row Galaxies of the Hyperreal Numbers Universe

TL;DR

Modern AI desperately needs second derivatives where it actually hurts- self-driving, medical models, finance - but the usual way of getting them is so expensive and fragile you can’t use them on billion-parameter systems without everything collapsing under compute and tooling overhead.

This article shows how to fix that with dual/jet algebra + compositional JVP ∘ VJP:

Hyperreals - think derivatives as ratios of infinitesimals, not limits-to-zero exam tricks
Duals & jets - computable infinitesimals: ℝ[ε]/(ε²) → duals , ℝ[ε]/(εᵏ⁺¹) → jets, where derivatives and higher orders are exact algebraic coefficients, not finite-difference noise.
Compositional autodiff - treat jvp and vjp as algebraic building blocks so JVP ∘ VJP gives you real second-order operators (H·v, local Taylor models) for roughly the cost of a couple of gradients, instead of O(n²) Hessian madness.

Yeah, PyTorch and JAX have grad, jvp, vjp.
But in practice, the overhead and tooling pain mean almost nobody uses second-order AD seriously at scale - it all gets treated like a give me a gradient button, not the dual/jet geometry engine it could be.

Payoff: With this approach, “normally expensive” second derivatives (HVPs) behave like cheap first derivatives, even on billion-parameter models - so you finally get real geometry and real mathematical guarantees to attack the actual hard problems: self-driving glitches, brittle medical models, financial blow-ups. No more hallucinations in first-order PyTorch/JAX vibes.

Why Your Calculus Is Lying to You

The limit-based calculus currently used in AI operates entirely in ℝ and thus fakes infinitesimals.

Cauchy and Weierstrass screwed up how we analyze continuous functions by replacing infinitesimals with limits:

f’(x) = lim[h→0] (f(x+h) - f(x))/h

Translation: “We can’t handle actual infinitesimals, so let’s pretend we’re getting close enough.”

In the 1800s? Sure, brilliant workaround. In 2025, when you’re computing derivatives across billions of parameters per second? Catastrophically obsolete.

Don’t believe me? Look at the plot below - and this is just a toy example. Real models? Much worse: absurd oscillatory calculus instead of the direct, easy solution you’ll learn in this story(dual numbers).

**Chart 1. Dual Numbers vs Finite Differences — Computing f′(1) for f(x) = x²Green line (dual numbers)**: exact answer (2.00) for any step size — no guessing required. **Brown dots (finite differences**): alternating between forward difference (overshoots) and backward difference (undershoots); the oscillation shows the “double guessing game,” where you must pick both a step size and which approximation formula to use. As h decreases (left to right), both methods converge toward 2.00 but never reach it exactly. The problem: your GPU plays this guessing game billions of times per second, which is why training is slow and loss curves zigzag. **The fix: dual numbers carry derivatives algebraically — no approximation, no step size, no formula selection, just the exact answer.** Note: x-axis inverted (large h → small h) to show the refinement story naturally. Plot by the author.

The limit-based calculus currently used in AI operates entirely in ℝ and thus fakes infinitesimals.

Cauchy and Weierstrass screwed up how we analyze continuous functions by replacing infinitesimals with limits:

f’(x) = lim[h→0] (f(x+h) - f(x))/h

Translation: “We can’t handle actual infinitesimals, so let’s pretend we’re getting close enough.”

In the 1800s? Sure, brilliant workaround. In 2025, when you’re computing derivatives across billions of parameters per second? Catastrophically obsolete. See the plot above

Here’s the irony: we’re finally circling back to what Newton and Leibniz actually wanted.

Newton: Fluents/fluxions — calculus as flowing quantities with instantaneous rates
Leibniz: True infinitesimals — algebra that captures the “infinitely small”

Both were right. The limit-based detour was a temporary hack because 19th-century mathematicians couldn’t rigorously define infinitesimals yet.

Three centuries later, YES WE CAN.

Hyperreals give infinitesimals a rigorous foundation. On machines, we use their finite engines — dual and jet algebras — to carry derivatives (and curvature) directly through computation.

No limits. No approximations. No lies.

This is calculus the way it was supposed to work, before we compromised because the math wasn’t ready yet.

Now it is. And your GPU deserves better than 200-year-old workarounds.

The Showdown: True Infinitesimals vs. Fake Limits

Time to step onto solid ground — number theory and algebra that actually work — and leave behind the 19th-century limit-based theater that’s been running your AI into the ground.

Forget the flat number line of the Real Numbers ( ℝ ).

That line was the foundation of the Archimedean empire — a world where everything had to be measured by stacking finite steps, where “limits” were invented to fake what infinitesimals actually are.

We don’t have to pretend anymore.

Welcome to the Hyperreal Numbers Universe (∗ℝ) — the long-overdue replacement for the broken real number system your AI is currently dying on.

Why Reals Can’t Cut It (And Why Your Models Keep Exploding)

The Real Numbers (ℝ) can’t represent infinitesimals or true infinities.

They flatten everything into one fragile, linear scale. No room for the infinitely small. No room for the infinitely large. Just a tight little rope you’re forced to balance on.

And that’s exactly why AI keeps breaking:

Gradients vanish → model stops learning
Values explode → NaN city, population: your training run
You’re stuck oscillating between “too small to matter” and “too big to handle”

The Hyperreal field (∗ℝ) fixes this catastrophe.

It restores the full spectrum of scale — from the infinitesimally small (ε) to the infinitely large (ω) — and gives calculus back its missing architecture.

Stop for a moment and picture that:

A number system wide enough to handle every scale that nature — and intelligence — can throw at it.

Not “close enough.” Not “approximate.” Actually there.

That’s what your GPU deserves. That’s what hyperreals deliver.

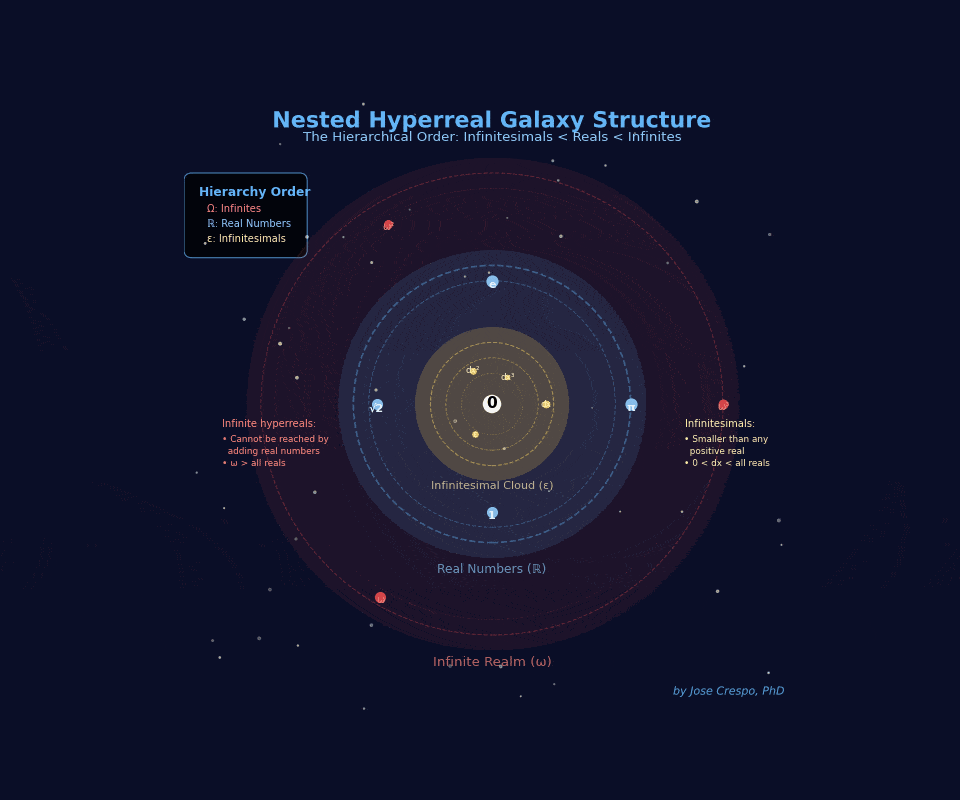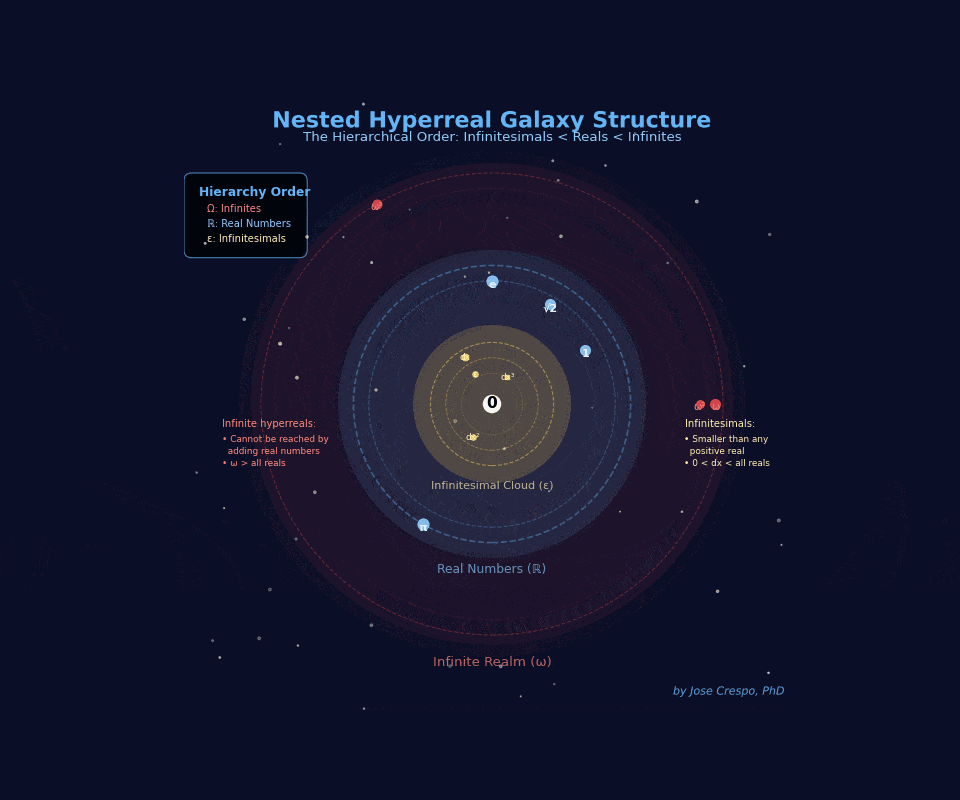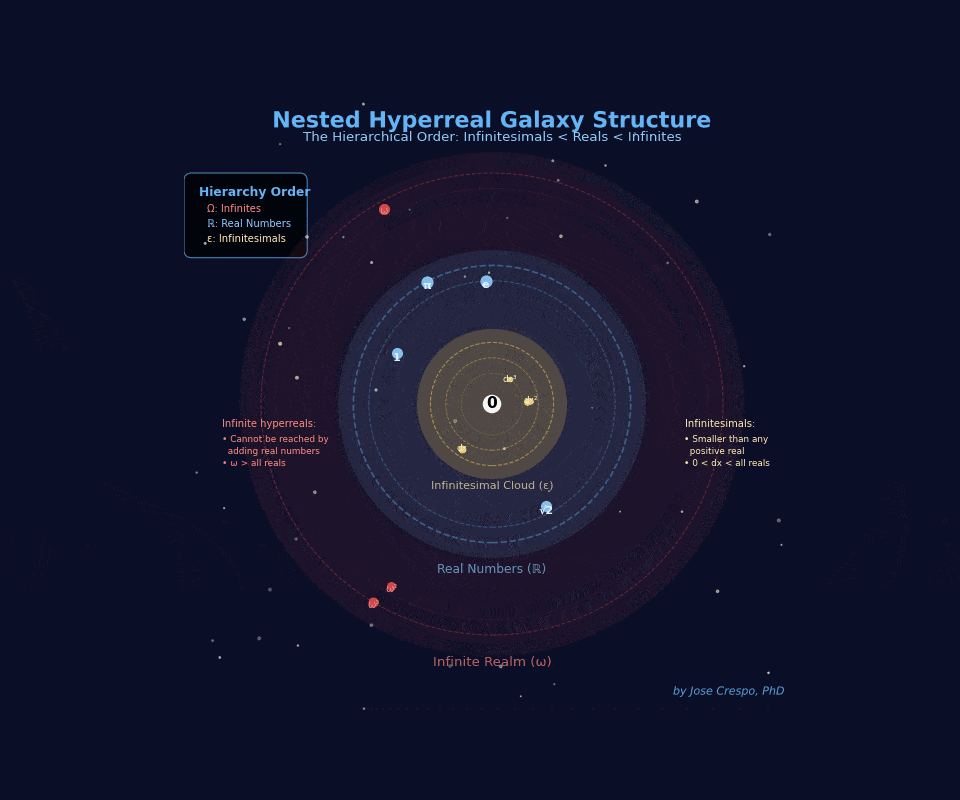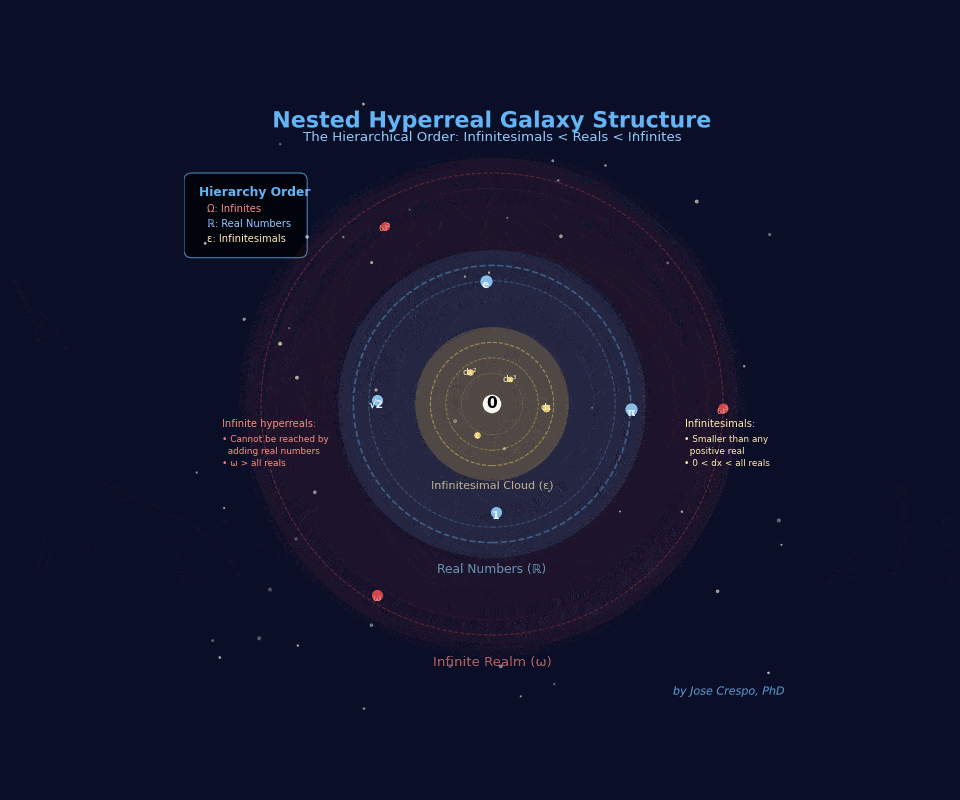
The Galaxy View: Understanding Hyperreals Visually

The hyperreal universe isn’t a number line — it’s a galaxy cluster.

Each disk is an entire realm of magnitude, separated not by distance but by mathematical impossibility. You can’t walk from one to another. You either have access or you don’t.

**Chart 2. The Row Galaxies of the Hyperreal Numbers Universe.** An animated view of the Hyperreal field shown as a row of galaxies. Each disk represents a realm of magnitudes within the Hyperreal superset — the extended number system that includes all reals, plus the infinitesimal and infinite scales the reals could never hold. Galaxy ε on the left is the infinitesimal cloud; Galaxy ℝ in the center is the finite realm of limited magnitudes (all real numbers and their halos); and Galaxy ω on the right stands for the infinite hyperreals. The pulsating halos trace the living boundaries between these regimes — zones approached through endless refinement or growth but never crossed by finite steps. Even the halos of each real number pulse, showing that every real is surrounded by its own infinitesimal cloud — values infinitely close yet never identical. They replace static geometric distance with a breathing sense of scale in motion — the heartbeat of the Hyperreal Universe. GIF created by the author with Stable Diffusion.

Meet the three galaxies your AI needs:

Galaxy ε (left) — The Infinitesimal Cloud
Numbers smaller than any real, yet still not zero. This is where dual numbers live. This is where exact derivatives happen. Your current AI can’t access this galaxy… it fakes it with limits.

Galaxy ℝ (middle) — The Finite Realm
All ordinary reals and their infinitesimal halos (the Monads of 1, π, e, …). Your AI is trapped here, pretending the other galaxies don’t exist. Every real number pulses with its own infinitesimal cloud, values infinitely close but never identical.

Galaxy ω (right) — The Infinite Realm
The domain no finite number can ever reach. Unbounded scale without explosions. Asymptotic behavior you can actually use.

Critical insight: The dashed axis isn’t a ruler. It’s a logical ordering, not a geometric distance.

You can’t slide from ε to 1 by taking small steps. You can’t reach ω by adding big numbers. The Archimedean ruler — the idea that everything can be measured by stacking finite pieces — breaks here.

Geometry collapses. Only hierarchy survives.

This is why limit-based calculus fails: it tries to reach infinitesimals by making finite numbers smaller (h → 0). But infinitesimals aren’t “really small reals”… they’re a different galaxy entirely.

Hyperreal algebra gives you direct access to all three. No approximation. No pretending.

Your GPU deserves to compute in the full universe, not just the middle ring.

But That Row of Galaxies Was Only a Teaser

It shows where each realm sits, but not how they connect.

The Hyperreal Universe isn’t flat — it’s layered. Think less “number line,” more “onion of scales,” each world wrapped inside another.

Here’s the main idea: those distances mean nothing.

You can’t slide from ε to 1, or from 1 to ω, by taking steps. The Archimedean ruler — the idea that everything can be reached by adding enough finite pieces — breaks here completely.

Geometry collapses. Only order remains.

Chart 3 reveals the truth.

If Chart 2 showed the map, Chart 3 reveals the laws of hyperreal gravity — how the entire Hyperreal Universe holds together around its silent core: 0.

The galaxies stop lining up and start nesting. The infinitesimal cloud (Galaxy ε) sits at the center, surrounded by the finite realm (Galaxy ℝ), which itself is engulfed by the infinite galaxies (ω, ω², …)

**Chart 3. The Nested, Pulsating Galaxies of the Hyperreal Numbers Universe**.An animated view of the hierarchy of scale inside the hyperreal field. Every orbit revolves around 0, the symbolic core of all monads. Galaxy ε forms the infinitesimal cloud, Galaxy ℝ the finite realm of limited magnitudes (all real numbers and their halos), and Galaxy ω the domain of infinite values beyond reach. The pulsating halos mark the living frontiers between realms — approached through endless refinement but never crossed by finite steps. They replace static Archimedean distance with motion in time, turning geometry into the rhythm of the infinite.GIF created by the author with Stable Diffusion.

Hyperreals in Action for Programmers

We’ve seen the shape of the hyperreal universe. Pretty galaxies, pulsating halos… all very philosophical.

Now let’s make it compute.

To turn that geometry into usable algebra, we need something programmable, differentiable, and verifiable. We must formalize what lives inside each “galaxy” of numbers.

1. The Definition That Newton Dreamed Of

Work inside ∗ℝ: the real numbers extended with non-zero infinitesimals.

Here’s the compact definition that took mathematics three centuries to rediscover!

ε ∈ ∗ℝ  such that  0 < |ε| < 1/n  for all n ∈ ℕ

0 limits. No guessing. Just a number smaller than any fraction of reals: a true infinitesimal.

This single idea resurrects Newton’s intuition and fixes the broken calculus that modern AI still runs on.

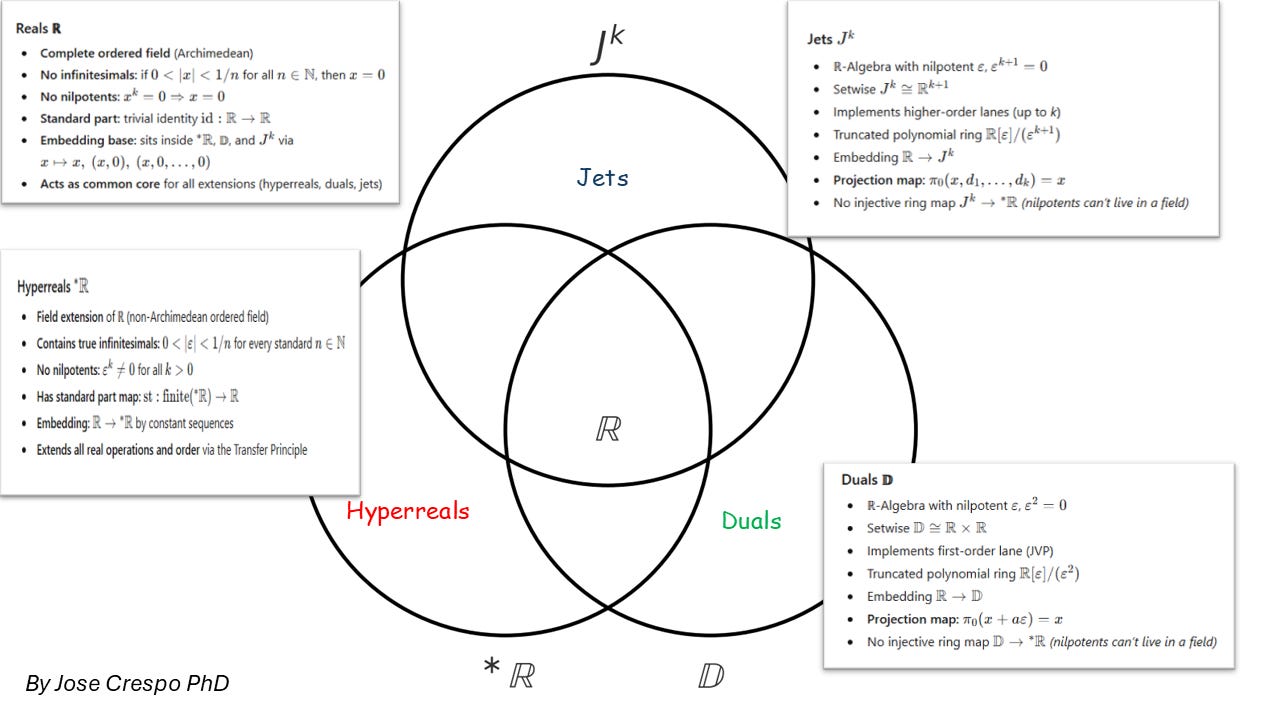
2. The Taxonomy of Fields Inside the Hyperreal Superset

(Or: the four number systems every serious AI engineer should secretly be using)

Let’s get practical.

Behind all that galaxy talk, we’re really dealing with four kinds of numbers; the ones that can actually change the way you build and train AI.

Each of these number systems — real, hyperreal, dual, jet — forms its own algebraic habitat, obeying different group, ring, and field laws. They’re not abstract nonsense; they’re layers of algebra that shape how your program handles motion, precision, and learning.

Think of them as four habitats in one mathematical ecosystem, each with its own physics: from the plain reals we’ve always used, to the hyperreals that define infinitesimals, down to the duals and jets that finally make all this computable.

One Universe, Four Number Forces

At the center sits the real numbers (ℝ) — the baseline arithmetic of every model and matrix multiply.

Extend them once, and you get the hyperreals (∗ℝ), the true mathematical universe that contains both infinitesimals and infinities.

Project a simplified, finite version of that same idea, and you arrive at the dual numbers (𝔻) and jets (Jᵏ) — the algebraic workhorses that make automatic differentiation possible.

In the set-theoretic view:

ℝ ⊂ ∗ℝ
ℝ ⊂ 𝔻
ℝ ⊂ Jᵏ

All four live in the same universe of structure… but their rules differ radically.

To Be or Not to Be Nilpotent

Here’s where the roads split.

Hyperreals (∗ℝ)

A field, perfectly ordered, no zero divisors.

That means no nilpotents — no “magic” numbers that vanish when squared or cubed.

Their infinitesimals ε are real elements in the algebraic sense:

ε² ≠ 0,  ε³ ≠ 0,  εⁿ ≠ 0  for all n

They’re tiny — smaller than any real fraction — but never zero.

Duals (𝔻) and Jets (Jᵏ)

These are rings, not fields, and they do contain nilpotents — elements that die after a few powers.

For duals:  ε² = 0
For jets:   εᵏ⁺¹ = 0

These nilpotents are algebraic doppelgängers of infinitesimals: not “real” in a field-theoretic sense, but powerful tools for derivatives. They gauge infinitesimal behavior just enough to automate calculus inside your code.

So the fact that nilpotents exist in duals/jets but are forbidden in the hyperreals is the deep structural divide.

Hyperreals: true infinitesimals, no nilpotents
Duals & Jets: nilpotent gauged infinitesimals, no field structure

Standard Part vs. Projection — How They “Return” to Reals

Now, how do we come back to normal reals after playing in these extended worlds?

In the hyperreals, we use the standard-part map:

st: ∗ℝ → ℝ

It collapses the infinitesimal halo:

st(x + ε·δ) = x  for any finite x and infinitesimal δ

That’s the real number your hyperreal was infinitely close to.

In duals and jets, there’s no notion of infinitely close, because these are algebraic rings, not ordered fields. So we use the simpler projection:

π₀: 𝔻 → ℝ  or  π₀: Jᵏ → ℝ

In plain English: just grab the value lane and ignore the derivative lanes.

Programmer shortcut:

st(·) → “take the real shadow” (hyperreals)
π₀(·) → “take the first component” (duals/jets)

Summary:

In ∗ℝ, infinitesimals are real field elements, with true proximity and a genuine standard part.

In 𝔻 and Jᵏ, ε-parts are nilpotent coefficients that vanish by projection — no infinite closeness, just algebraic bookkeeping.

Why This Matters for AI

Hyperreals give us the ideal semantics of calculus: the way derivatives and limits were meant to behave before we replaced them with fragile ε–δ tricks.

Duals and jets give us the machine algebra to compute those derivatives exactly, without symbolic headaches or numerical jitter.

When you lift a real input x into a jet:

x̂ = x + d₁·ε + (d₂/2!)·ε² + ...

and run your usual forward pass, you’re literally running your program over a truncated Taylor ring.

At the end, you project back:

value in lane 0
gradient in lane 1
curvature in lane 2
and so on

That’s how real code gets exact calculus.

So here’s the simple rule of thumb:

Hyperreals explain calculus
Duals and jets compute it

The first gives meaning, the second gives power.

Algebra: The Rules to Play the AI Game with Hyperreals

Alright, time to stop orbiting theory and touch the ground.

We’ve mapped the Four Number Forces: Reals, Hyperreals, Duals, and Jets. Now we build the algebra that actually makes them move.

This is where abstract structure turns into computation.

The Hyperreals give you the truth of calculus, infinitesimals included.

Duals and Jets give you the machinery, the algebraic engines that make that truth computable.

Think of it like this:

Hyperreals are the blueprint
Duals and Jets are the compiler

We’ll move step by step: from pure infinitesimals to first derivatives to curvature.

By the end, you’ll see that automatic differentiation — the core of modern AI — is nothing more than hyperreal algebra disguised as code.

1. Hyperreal Infinitesimals — The Conceptual Ground Truth

f’(x) = st((f(x+ε) - f(x))/ε)

Here, st(·) means standard part: it removes the infinitesimal tail.

We don’t simulate ∗ℝ directly: we build a finite algebra that reproduces its derivative behavior exactly.

2. Dual Numbers (k = 1)

Elements:

x̂ = x + d₁·ε   with   ε² = 0

Arithmetic:

(x + a·ε) + (y + b·ε) = (x + y) + (a + b)·ε

(x + a·ε) · (y + b·ε) = (x·y) + (x·b + a·y)·ε     # product rule appears

Constants lift as (c, 0).

Functions (first order)

The coefficient of ε is the directional derivative (JVP):

For smooth f:

f(x + d₁·ε) = f(x) + f’(x)·d₁·ε

Programming recipe:

Represent a scalar as (x, d₁)
Set d₁ = 1 to get ∂f/∂x, or use a direction vector v to get Jf(x)·v
Implement + and * once—everything else flows automatically
Cost: about 2–3× a normal forward pass

3. Jets (k = n ≥ 2)

Duals give you slopes. Jets give you curvature and higher-order awareness.

Elements:

x̂ = x + d₁·ε + (d₂/2!)·ε² + ... + (dₙ/n!)·εⁿ
with εⁿ⁺¹ = 0

Arithmetic (up to order 2):

(Ax, A₁, A₂) * (Bx, B₁, B₂) =
( Ax·Bx,
  A₁·Bx + Ax·B₁,
  A₂·Bx + 2·A₁·B₁ + Ax·B₂ )

Functions (order n):

f(x + d₁·ε + d₂·ε²/2!) = f(x) + f’(x)·d₁·ε + f’‘(x)·d₂·ε²/2! + ...

Each power of ε carries one derivative order.

It’s like a multi-lane Taylor engine where curvature, acceleration, and higher changes flow in parallel.

Why this matters:

Jet² gives Hessian-vector products (HVPs) and Newton/TR steps without explicitly building a Hessian
Higher-order Jets (J³, J⁴, …) give full Taylor expansions in one pass — vital for control, simulation, and meta-learning

So What Do I Actually Do With This on Monday?

Dual/jet algebra + compositional functors (JVP ∘ VJP) is one of the only viable ways to get exact, composable second-order math anywhere near billion-parameter, real-world AI.
The way PyTorch/JAX are actually used today is a tiny, first-order slice of that potential.

Right now PyTorch/JAX can do grad, jvp, vjp, even jvp(grad(f), …) – but:

they’re treated in practice as give me a gradient buttons,
second-order is bolted on as an afterthought (slow, awkward, mostly limited to small-scale experiments),
almost nobody designs training, safety, or debugging around curvature because it’s too painful to use systematically on large systems.

Dual/jet algebra is the upgrade:

Derivatives become exact algebraic objects, not some tensor the lib spat out once.
JVP and VJP are understood as functors on that algebra, so JVP ∘ VJP is by construction a genuine HVP operator, not a fragile API trick.

Once you think this way, you can:

localize second order (per block, per subsystem, per semantic direction), so you only pay the ~2–3× cost where it matters,
and later bake jets into the backend (C++/CUDA with real jet types and fused kernels) so those same compositional operations stop being research toys and become everyday tools.

That’s the scaling story:

Naive PyTorch/JAX usage: a first-order culture where second-order is technically possible but ergonomically and computationally painful on big, realistic models.
Dual/jet-based, compositional design: Same asymptotic cost, but now you can point real second derivatives at the mess created by first-order-only vibes in self-driving, medical AI, finance, and other billion-parameter monsters, without your stack collapsing under PyTorch/JAX overhead and tooling friction.