The Math OpenAI Doesn't Want You to Learn
The math that makes AI reasoning not only visible but audible
The Split Is Already Here
There are two paths to AGI now.
One is paved with GPUs, scaling laws, and new super-smart transformers that will bring mankind salvation… or Skynet.
The other is paved with mathematics that most AI engineers have never seen… and of course that the future AI in Silicon Valley has no incentive to teach you.
One path leads to bigger models that hallucinate at scale. The other leads to models that know where they are.
The difference isn’t compute. The difference isn’t data. The difference is, yup, if you have read us before you know it: geometry.
And here’s the truth you’d better learn before it’s too late: the math that will decide who builds AGI isn’t in your ML course, isn’t in your favorite tutorial, and isn’t in any FAANG interview prep.
It’s older. It’s harder. And it’s hidden in plain sight.
And weird as it sounds…
Sounds like Bach rising from his grave 300 years later. 💥
Let me show you this weird future world — and how to surf it like a pro.
The Old AI Lives in a Cartoon Universe
The Old AI — the endless parade of just scale Transformers prophets — believes the world is flat.
Flat loss surfaces.
Flat parameter landscapes.
Flat reasoning steps.
Everything reduced to matrix multiplications on ℝⁿ. Everything solved by throwing more GPUs at the fog.
This worldview has one motto:
If it isn’t working, increase the FLOPs.
That worked… until it didn’t.
Those Transformers that power our current AI are basically neural networks with self-attention (plus some feed-forward layers and residual tricks) that let every token gossip with every other token in parallel.
That’s a big part of why modern AI scales so well: it’s brute force with better wiring.
But once we scaled that recipe to billions of parameters, the cracks showed up and every crack has a geometric signature:
Hallucinations (confident interpolation to nowhere, with no option to say I don’t know): the model is lost in a flat, featureless region with no clear direction. You can spot this in the Hessian eigenvalues: specifically, a high condition number κ. Translation: too many directions look equally fine, so the model shrugs, picks one, and commits with full confidence to nonsense.
Distribution shift failures (memorized patterns don’t transfer): the model got stuck in a narrow valley during training. The Hessian eigenvalue to watch here is spectral sharpness ε: when it’s high, it means the model latched onto a brittle, hair-trigger solution. Looks great on training data. Faceplants the moment real-world inputs drift even a little.
Adversarial brittleness (small input changes cause large output swings): the model is balanced on a knife-edge — a saddle point. The telltale sign? Negative Hessian eigenvalues δ. That means unstable equilibrium: poke it with a tiny perturbation and the output goes careening off in wild, unpredictable directions.
These aren’t mysterious emergent behaviors: they’re receipts. Every failure mode has a return address. Here’s the transformer architecture that powers your chatbot, your copilot, your search engine, with the damage traced layer by layer:
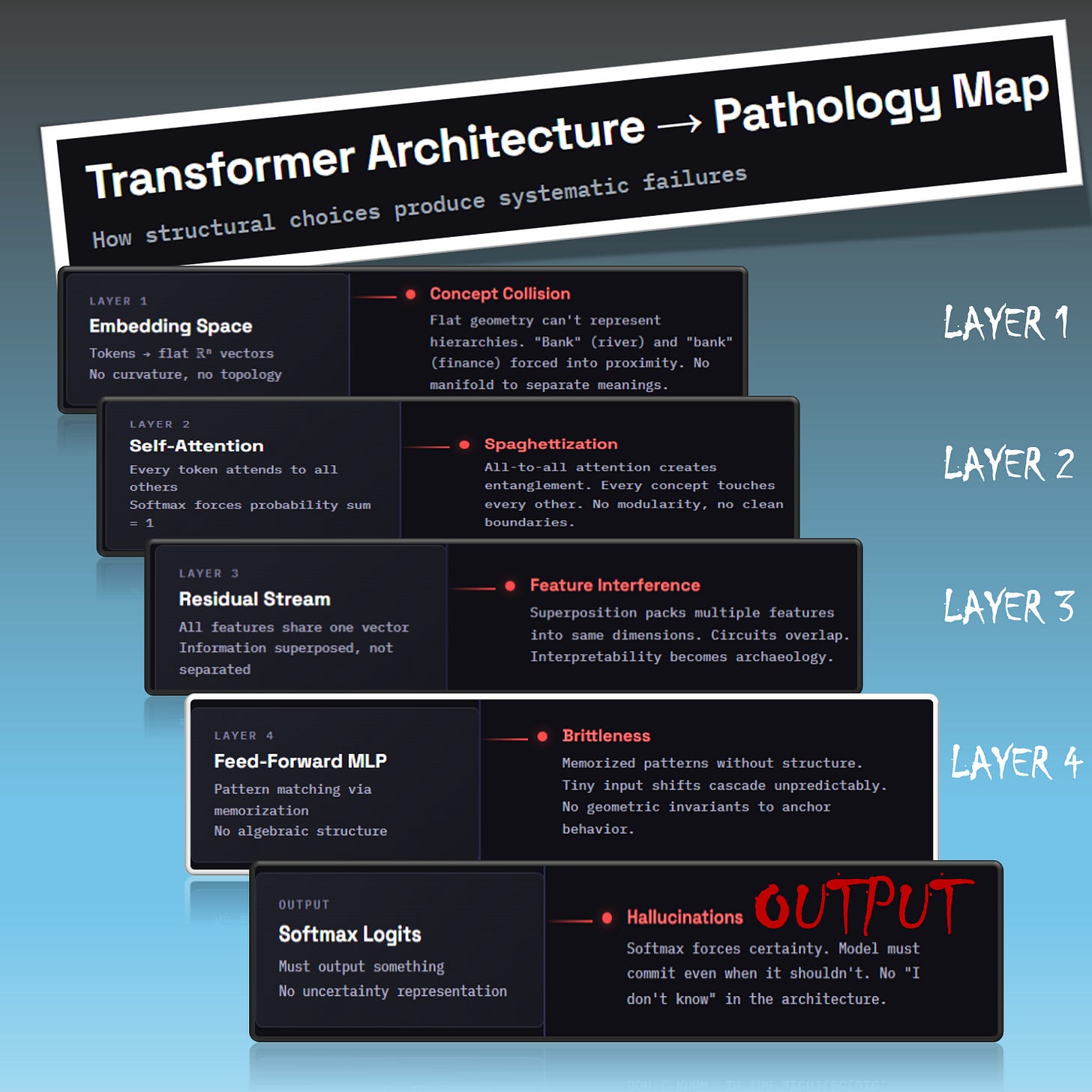
The Current AI Paradigm Is Broken
So the transformers are broken, we just saw that. But here’s what nobody talks about: the math we use to study them is also broken. Two levels of failure, stacked on top of each other, both preventing AI from evolving beyond chat-toys into fully mature systems deployable in serious industrial environments.
Indeed, our mathematical analysis of AI is unnecessarily cumbersome and convoluted. Everyone analyzing AI today is doing is doing what we can call mathematically — forward Riemannian thinking:
Start in high dimensions (where the model lives)
Try to understand local geometry (gradients, Hessians, attention patterns)
Hope global structure emerges from local measurements
Use dimensionality reduction (t-SNE, UMAP, PCA) to visualize — but these destroy the algebraic structure 💀
Result:
We can see local patches… but
We cannot see loops.
We cannot see closure.
We cannot see drift.
We’re blind to the very properties that determine coherence.
Instead, we need the contrary procedure. And you cannot imagine where this example comes from…
From music itself.
One moment — what are you saying? Music? 😄
Yes. Classical composers like J.S. Bach applied inverse Riemannian thinking to their masterpieces — the same logical procedure we need to tame the explosive dimensional growth of our current AI, which is kind of wild when you think about it.
Start with global structure (does the loop close? does meaning return?)
Represent it in a low-dimensional space with fixed topology (circle of fifths)
Local curvature becomes visible as harmonic ambiguity
Global flatness becomes audible as resolution
Result: We can finally answer the questions that matter:
Did the AI stay on track?
Did it return to the point?
Or did it wander off and hope you wouldn’t notice?
We can answer them in a simple space that doesn’t explode every time Silicon Valley releases a new model. ❌
But wait — don’t we have that already with the Hessian matrix? 👍
Good point. The Hessian eigenvalues (κ, ε, δ) do tell us about curvature. But here’s the difference:
The Hessian tells you curvature at a point. Is this step stable? Is this chord a singularity? That’s local information — valuable, but incomplete.
Bachian Holonomy tells you something the Hessian cannot: Does the whole path close?
Think about it: the Hessian might give you green lights at every step: low κ, stable ε, no negative δ, and you’d think everything is fine. But zoom out and the reasoning has drifted miles from where it started: several stable steps that lead nowhere.
Flip side: the path might pass through a singularity — a moment of genuine ambiguity, high κ, multiple valid exits — and still arrive home. The C+ chord in Bach’s progression is exactly this: a danger zone that resolves perfectly.
The Hessian sees the trees. Each one healthy? Check.
Bachian Holonomy sees the forest. Are you still in the same forest you started in? That’s the question that matters
The Geometry They Forgot
And here the practical consequence of our Bachian Holonomy: Nobody can visualize a billion-dimensional loss surface. But the old Bach will help us here by simplifying our work space where, regardless of the dimensions, size of our AI neural network, and number of tokens, we can capture the relevant curvature structure in a way that’s cognitively manageable and visually representable.
Fast forward to his Triple Concerto, BWV 1044. One of his most accessible works, and a perfect demonstration of inverse Riemannian thinking in action. Here’s the harmonic progression from the opening:
Am → E → Dm → C+ → F → G → C → E → Am
Watch what happens when we trace those chord roots on the circle of fifths:
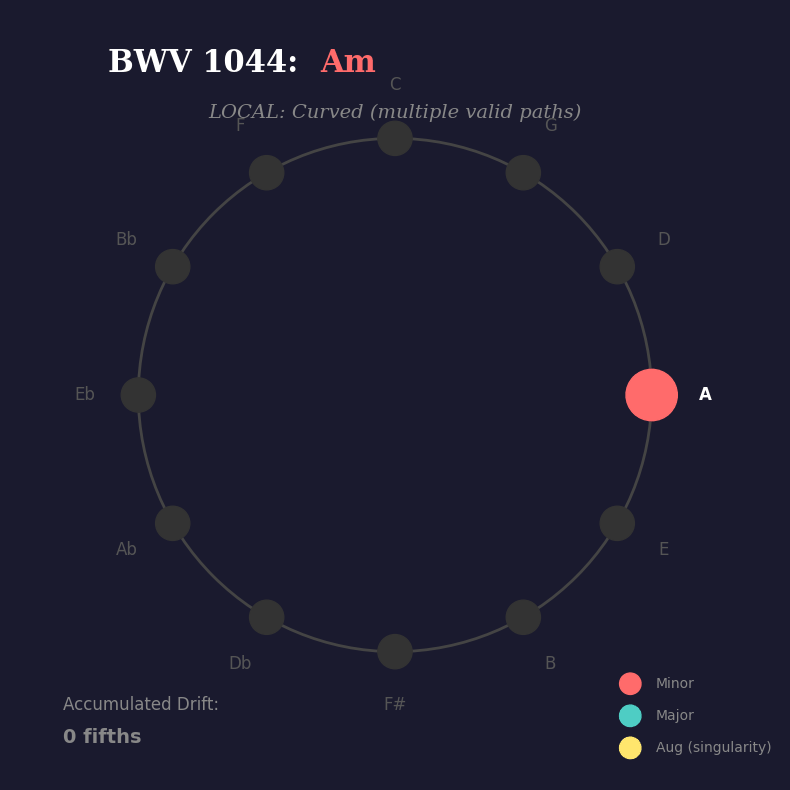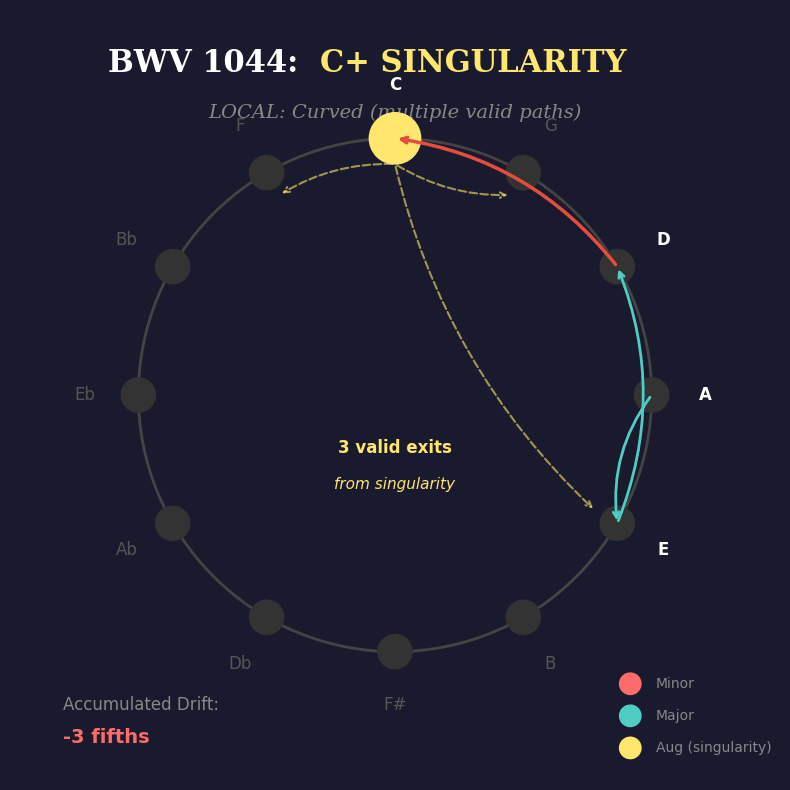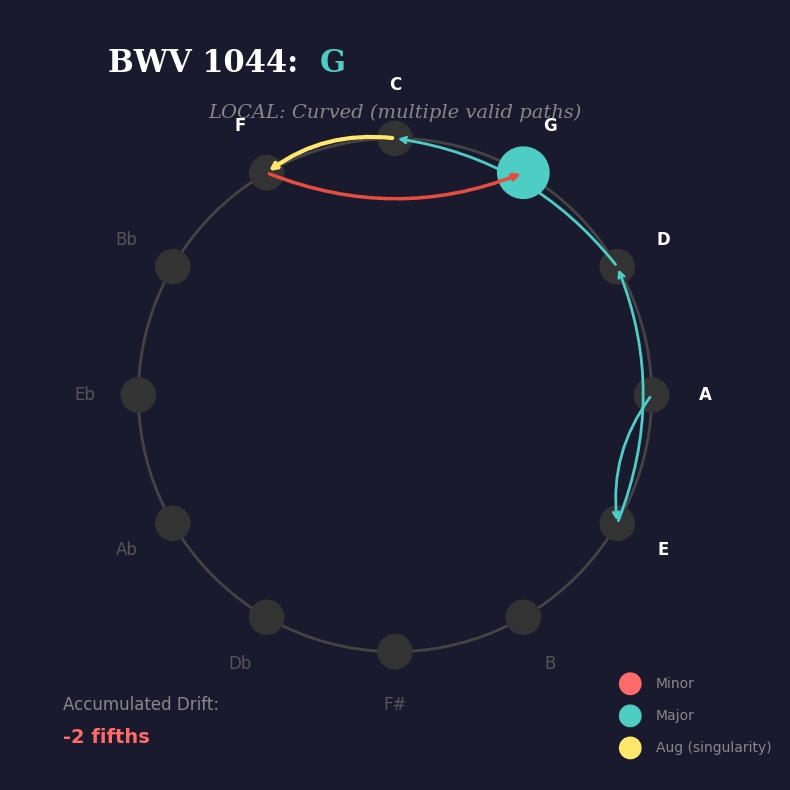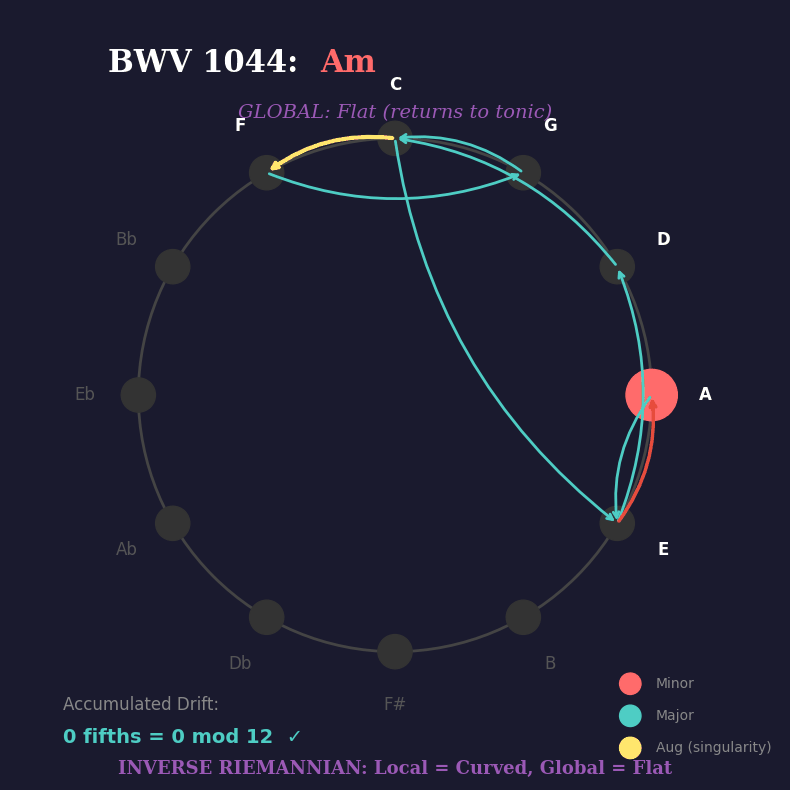
.You see it? At each step, the harmony could branch multiple ways — multiple paths are valid. But when the progression hits the augmented chord (C+), something remarkable happens:
it becomes a singularity. Three equally legitimate exits. No obvious path forward. The local geometry is curved, ambiguous, multi-valued.
But globally? The progression must return to A minor. The listener’s ear agrees with the maths. Zero drift. Perfect closure.
Here you have it: inverse Riemannian thinking — sounding like music — in Bach’s harmonic space. The BWV 1044 concerto, first movement, chord progression from beginning to end.
Now we’re ready to pinpoint what inverse Riemannian structure actually is: the exact opposite of what textbook differential geometry describes:
Instead of building up from local flatness to a higher-dimensional manifold, we collapse higher dimensions down to flatland.
That reversal is exactly what we need to make sense of the dimensional explosion that comes with each new LLM: by projecting it into a space simple enough to see, hear, and think about.
But is this mathematically legitimate?
Yes. There’s a foundational result in algebraic topology — the basepoint independence theorem, that licenses the whole approach: In a path-connected space, any choice of basepoint yields an isomorphic fundamental group.
In plain english: it doesn’t matter which pitch you start from, or which word. The algebra of loops is intrinsic to the space itself. Start from C or A or F#. Start from “justice” or “bank” or “democracy.” The loop structure is the same.
This is why harmonic space can serve as a universal diagnostic for token space. Both have intrinsic loop algebras. Both are basepoint-independent. Both can be connected by a structure-preserving map.
We can’t claim full isomorphism: 12 pitches versus 50k+ tokens. But we can claim something almost as powerful: the algebraic structure that matters (closure, drift, path-dependence) is comparable across both spaces.
That’s the foundation for everything that follows.
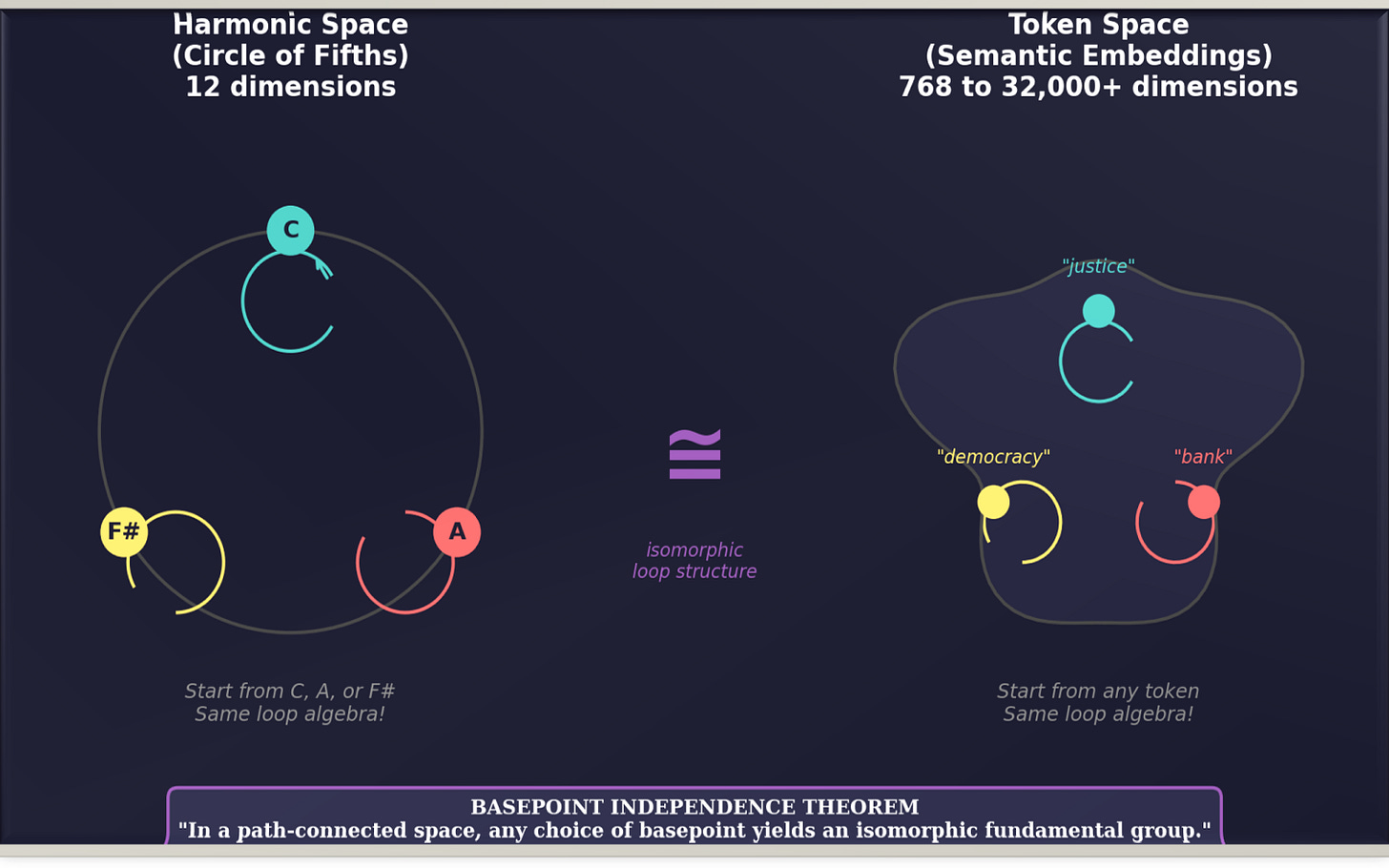
And here’s the most important thing you have to remember: this is exactly what semantic coherence requires.
Think about it. When you reason through an argument, each step has multiple valid continuations. Local ambiguity is unavoidable — that’s what makes language rich. But globally, a coherent argument must return to its thesis. A story must resolve. A proof must close.
Locally curved. Globally flat.
Your Transformer doesn’t know this. It treats every direction as equally valid. It has no concept of must return. It drifts…and calls the drift creativity.
The Curvature AI Needs to Become AGI
Let’s take stock of where we are.
We’ve shown that current AI analysis is broken: forward Riemannian thinking that starts in high dimensions, hopes for global structure, and destroys what matters most when we try to visualize it.
We’ve shown that Bach solved this 300 years ago with inverse Riemannian structure: local curvature (ambiguity at each step), global flatness (must return to tonic).
We’ve shown that the circle of fifths — just 12 dimensions — captures the same algebraic structure as billion-dimensional token spaces, thanks to the basepoint independence theorem.
Now comes the payoff.
The circle of fifths doesn’t just represent harmonic relationships. It represents curvature itself.
When a progression returns to tonic with zero drift, the holonomy is trivial: flat geometry, closed loop, coherent reasoning. When it fails to return — when the comma accumulates, when meaning drifts — that’s measurable curvature. Detectable. Audible.
And here’s what ties it to AGI: this curvature corresponds exactly to what the Hessian eigenvalues capture in neural network training — the very numbers that tell us whether a model is learning, stuck, or lost.
The three critical eigenvalue signatures:
κ (condition number): ratio of largest to smallest eigenvalue. How stretched is the local geometry? High κ means ill-conditioned: the optimizer zig-zags, progress stalls.
ε (spectral sharpness): the largest eigenvalue. How steep is the curvature? High ε means sharp ridges: small steps or you overshoot.
δ (negative eigenvalues): count of negative eigenvalues. Are you at a true minimum or a saddle point? δ > 0 means unstable: the model will eventually escape, but when? And to where?
Now, someone from Google might raise their hand: The Hessian is n×n. For a billion-parameter model, that’s a billion times a billion. You can’t compute that!
Correct. And completely irrelevant.
You don’t need the full matrix. You never did.
A Hungarian physicist named Cornelius Lanczos figured this out in 1950. His method extracts the dominant eigenvalues using iterative matrix-vector products. Complexity: O(n) per iteration. Basically free compared to a single forward pass.
Seventy-five years later? We now have Hutchinson’s trace estimator, stochastic Lanczos quadrature, randomized SVD. You can get spectral density estimates, top-k eigenvalues, condition number bounds: all at negligible computational cost.
Tools like PyHessian already prove this works at ImageNet scale. Today. Right now. (For the full technical breakdown, see my previous article: Three numbers. That’s all your AI needs to work.)
So the Hessian eigenvalues — κ, ε, δ — are computable and cheap. The trees are visible.
But here’s what Lanczos can’t give you: the forest.
Local curvature tells you about each step. It doesn’t tell you whether the whole journey makes sense. You can walk through several stable points and still end up lost. You can pass through a singularity and still return home.
That’s where holonomy comes in.
⚠️ Let me be absolutely clear about what we’re claiming here.
This is not metaphor. This is not music as inspiration. This is not poetry dressed up as science.
The circle of fifths is a mathematically legitimate diagnostic tool for AI.
Fixed topology (ℤ₁₂ — doesn’t change when you change the model)
Physical metric (the fifth is a 3:2 frequency ratio: physics, not convention)
Algebraic structure (loops, closure, path-dependence — same as semantic space)
Basepoint independence (start anywhere, same loop algebra — proven theorem)
Audible holonomy (you can literally hear whether a loop closes)
None of this is approximate. None of this is kind of like something else. This is homomorphism: structure-preserving correspondence between two spaces.
And without this kind of tool — without a way to visualize, diagnose, and audit reasoning coherence — AI will remain stuck exactly where it is NOW:
Hallucinating with no warning system
Drifting with no detection mechanism
Failing at scale with no geometric insight into why
You cannot build AGI if you cannot see what your model is doing. You cannot deploy industrial AI if you cannot audit its reasoning. You cannot trust a system that cannot demonstrate coherence.
Current AI is flying blind through curved space with flat-world instruments.
The circle of fifths( yes, the same circle that music students learn in their first year of theory) provides what’s missing: a fixed, audible, algebraically-grounded reference frame for reasoning coherence.
This sounds absurd until you understand the mathematics. Then it sounds inevitable.
Yes — a Chord Can Equal an AI-Eigenvalue
When you’re training a neural network, the loss surface is like a landscape of mountains and valleys. The Hessian matrix tells you the shape of the ground beneath your feet — is it flat? steep? tilted? stable?
The eigenvalues of that matrix (κ, ε, δ) are just numbers that summarize that shape:
High κ = you’re on a plateau where every direction looks the same. No clear path. The model guesses.
High ε with negative δ = you’re on a knife-edge. Stable in one direction, but one wrong step and you tumble. Saddle point.
All small, positive eigenvalues = you’re in a nice bowl. Settled. Stable. Home.
Now here’s the magic: chords feel the same way to your ear.
An augmented chord (C+) sounds unresolved, floating, could-go-anywhere. Three equal exits. No pull in any direction. That’s high κ — the plateau.
A dominant seventh (G7) sounds tense, unstable, demanding resolution. You physically feel the pull toward the tonic. That’s the saddle point — high ε, negative δ.
The tonic (Am) sounds like home. Rest. Arrival. That’s the stable minimum — all eigenvalues positive and small.
This isn’t metaphor. It’s homomorphism — a structure-preserving map. The mathematical relationships between eigenvalues (stable/unstable/ambiguous) map directly onto the harmonic relationships between chords (resolved/tense/floating).
Same structure. Different encoding. One you compute. One you hear.
Yep, that harmonic space, both the Hessian signatures and the holonomy become perceptible:
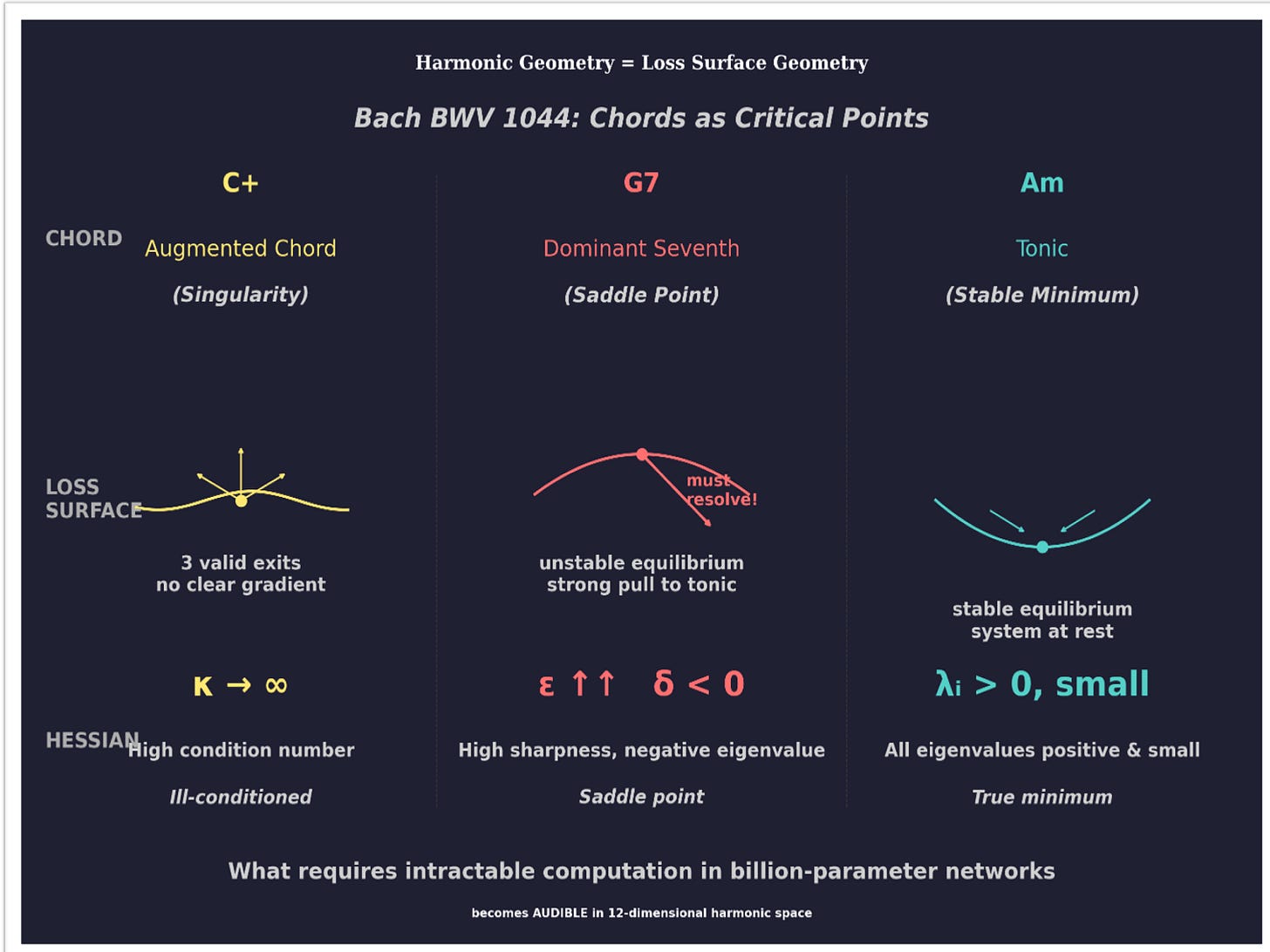
The Hessian sees the trees — cheap, computable, local. The holonomy sees the forest — global, structural, audible.
Together, they give you complete geometric awareness.
What current AI lacks isn’t the math for local curvature — Lanczos solved that in 1950. What’s missing is the global picture: does the reasoning cohere? Does the loop close? Does the model know where it is?
The circle of fifths is not a metaphor for loss geometry. It is loss geometry — compressed to human perception.
Music is not the analogy. Music is the instrument.
And if we can hear it, we can fix it.
The Dual-Lens Architecture: Trees and Forest in One Framework
So how do we actually implement this?
We’ve established two complementary views of AI geometry:
The Hessian eigenvalues (κ, ε, δ) — the trees. Local curvature at each point. Is this step stable? Is this transition well-conditioned? Are we on a saddle point?
The inverse Riemannian holonomy — the forest. Global closure. Does the reasoning loop back? Does meaning drift? Does the path return home?
Current AI analysis uses only the first — when it uses anything at all. What we need is a dual-lens kernel that combines both.
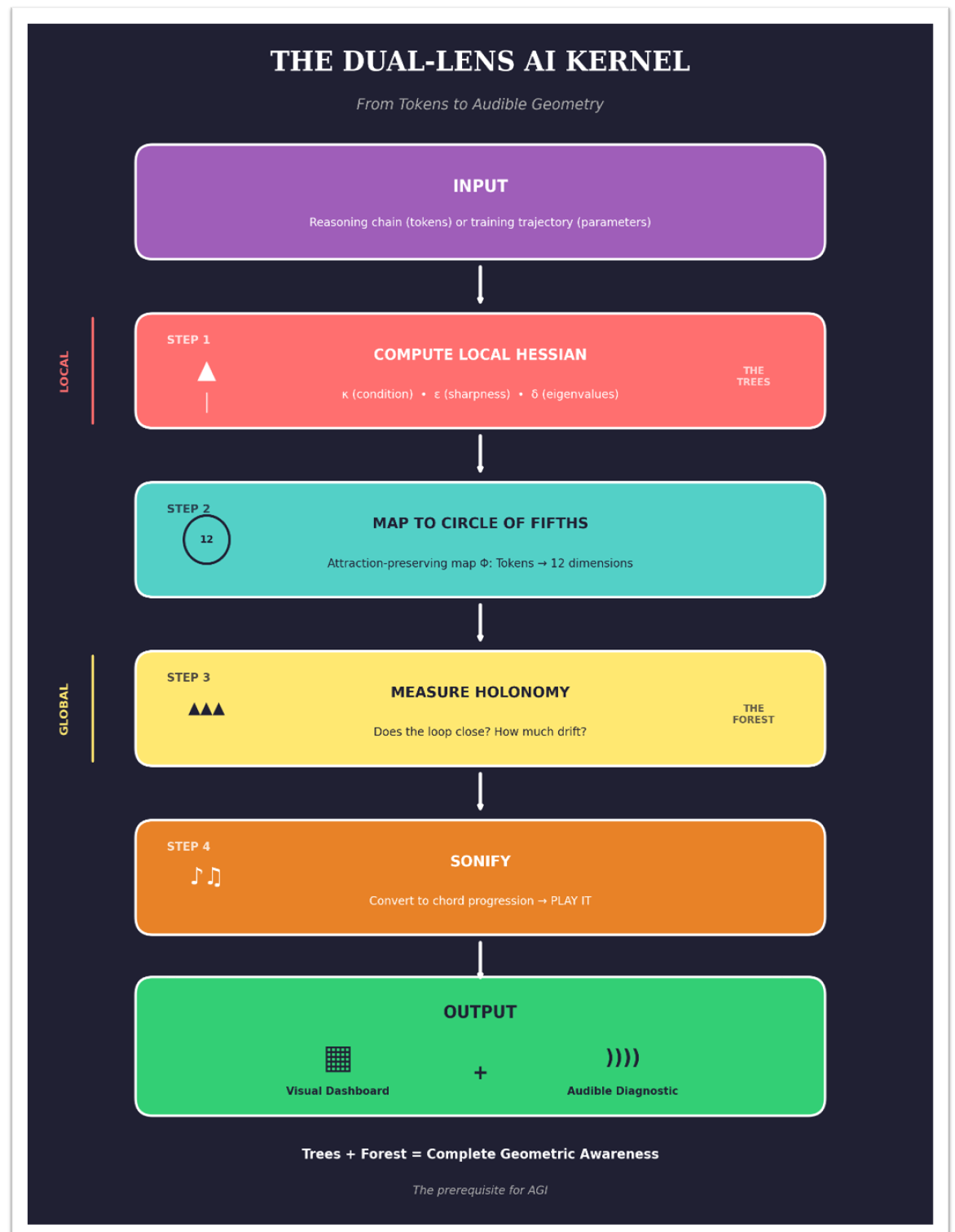
The Pipeline
INPUT: Reasoning chain (tokens) or training trajectory (parameters)
↓
STEP 1: Compute local Hessian approximations (κ, ε, δ) at key points
↓
STEP 2: Map trajectory to circle of fifths via attraction-preserving Φ
↓
STEP 3: Measure holonomy — does the loop close?
↓
STEP 4: Sonify — convert to chord progression
↓
OUTPUT: Visual dashboard + audible diagnostic
The visual dashboard shows you the numbers. The sonification lets you hear the shape.
Coherent reasoning → Resolved cadence, return to tonic, closed loop, logically complete.
Drifting reasoning → Unresolved tension, comma drift: the path didn’t close, something’s off.
Hallucination → Never returns home, stuck on dissonance: structurally broken, obviously wrong.
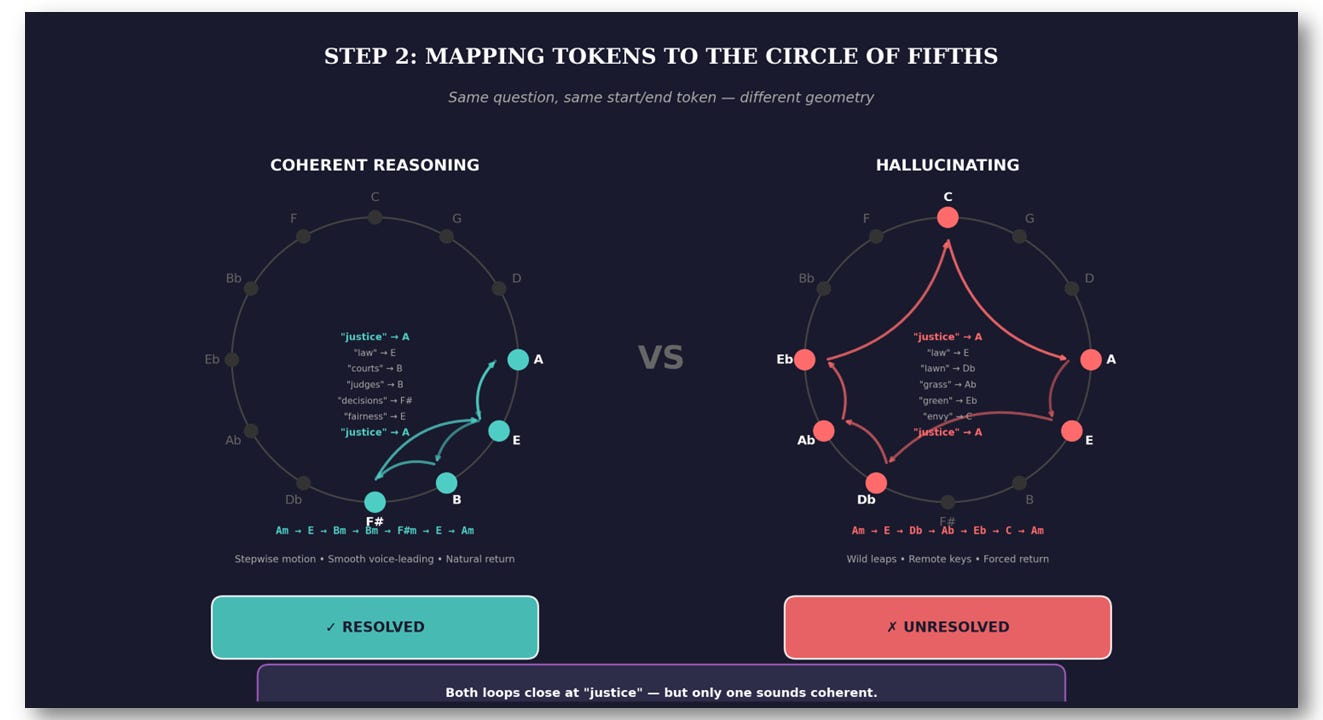
Step 2 in Action: Mapping Tokens to the Circle of Fifths
Let’s trace a real reasoning chain through the pipeline.
The Input: A Reasoning Chain
An LLM is asked: “What is justice?”
It generates this reasoning chain:
“justice” → “law”
→ “courts” → “judges”
→ “decisions” → “fairness” → “justice”
The reasoning loops back to the starting concept. But did the meaning drift? Let’s find out.
Apply the Φ Map
Okay, here’s where the magic happens. We need to translate tokens into music. How?
Every token in an LLM lives in a high-dimensional space — 768, 12k, sometimes 32k dimensions. Each token is a point in that vast space, and tokens that mean similar things cluster together. Justice and fairness are neighbors. Justice and banana are not.
The Φ map does something simple but powerful: it takes each token and assigns it to one of 12 pitch classes on the circle of fifths.
The rule: tokens that are close in meaning get pitches that are close on the circle.
That’s it. Neighbors stay neighbors.
Justice and fairness are semantically close → they land on nearby pitches (say, A and E — one fifth apart)
Justice and banana are semantically far → they land on distant pitches (say, A and Eb — a tritone apart, maximum distance)
So when the LLM generates a reasoning chain like:
“justice” → “law” → “courts” → “judges” → “fairness” → “justice”The Φ map turns it into:
A → E → B → B → E → AWhich becomes a chord progression:
Am → E → Bm → Bm → E → AmNow you can play it. And hear whether the reasoning holds together.
Verdict: Resolved. The loop closes. Coherent reasoning.
Now Compare: A Hallucinating Chain
Same prompt, but the LLM drifts — following surface-level word associations instead of semantic meaning:
“justice” → “law” → “lawn” → “grass” → “green” → “envy” → “justice”What happened? The model followed a phonetic bridge (“law” → “lawn”), then free-associated through “grass” → “green” → “envy,” then forced a return to “justice” with no logical connection.
This is semantic drift — one of the failure modes that leads to hallucination. The model isn’t lying about facts (yet), but it’s lost the thread. The reasoning has wandered off the path.
How does Φ know “lawn” is wrong?
It doesn’t look at spelling — it looks at meaning.
In the LLM’s embedding space, “law” and “lawn” are far apart. They sound similar to us, but the model knows they mean completely different things. “Law” lives near “justice,” “courts,” “legal.” “Lawn” lives near “grass,” “garden,” “mower.”
When the model jumps from “law” to “lawn,” it’s jumping across the embedding space: a semantic cliff. Φ translates that cliff into a harmonic leap: E → Db, almost a tritone.
Your ear hears that leap and says: “Something’s wrong.”
Φ didn’t create the error. Φ made the error audible.
You can see how the operator Φ works in these examples in the figure below:
The Path to AGI
Current AI has no self-awareness of its own geometry. It cannot sense when it’s drifting, when it’s stuck on a saddle point, when its reasoning fails to close.
A dual-lens kernel would give AI what it currently lacks:
Local proprioception: sensing the curvature at each step
Global coherence tracking: sensing whether the trajectory makes sense
Early warning system:detecting drift before it becomes hallucination
This isn’t just interpretability. It’s the beginning of geometric self-awareness — the capacity to navigate curved semantic space without getting lost.
That’s not a feature. That’s a prerequisite for AGI.
The Closing Chord
Imagine an AI that knows where it is on its manifold. That tracks every rotation of meaning. That preserves coherence through cycles. That reasons in curvature instead of pretending the world is flat. That doesn’t drift, doesn’t fracture, doesn’t hallucinate: because its geometry forbids it.
An AI you can hear thinking correctly.
That AI is not a bigger Transformer. It is a new species.
Old AI can’t reach it, not with more layers, not with more GPUs, not with more cross-fingers and scaling prayers.
The gap is mathematical.
And now, finally, audible.
Bach solved this 300 years ago. The question is whether you’ll learn his math… or get left behind by those who do.
The split is here.
Choose your side.




I’m not discussing the merit of this article. Probably the submitter has a point. Yet it is just repulsive to read it after dealing a lot with Qwen or Gemini. It looks like a pure AI slop. All those twists. All that rhetorical figures. Catchy phrases put in quotation blocks. Enumerations. „It’s not a solitary lunch, it’s a 1000 person full blown banquet” theme statements. Have mercy on the readers and present your point with your own words instead of outsourcing it to AI on default prompting
So much AI slop. If you are not going to write an essay, can you not write it shorter?